如图，平面直角坐标系中有一矩形纸片OABC，O为原点，点A,C分别在x 轴，y轴上，点B坐标为
（其中
），在BC边上选取适当的点E和点F，将
沿OE翻折，得到
；再将
沿AF翻折，恰好使点B与点G重合，得到
，且
．
（1）求
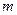的值；
（2）求过点O,G,A的抛物线的解析式和对称轴；
（3）在抛物线的对称轴上是否存在点P，使得
是等腰三角形？若不存在，请说明理由；若存在，直接答出所有满足条件的点
的坐标（不要求写出求解过程）．
如图，在梯形ABCD中，AD∥BC，∠B=90°,AD=18cm，BC=21cm，点P从点A开始沿AD边向D以1cm/s的速度移动，点Q从点C开始沿CB边向B以2cm/s的速度移动，如果P、Q分别从A、C同时出发，设移动的时间为t(s)，求：
（1）t为何值时，四边形PQCD为平行四边形；
（2）t为何值时，四边形ABQP为矩形；
（3）t为何值时，梯形PQCD是等腰梯形。
某数学兴趣小组在本校九年级学生中以“你最喜欢的一项体育运动”为主题进行了抽样调查，并将调查结果绘制成如图图表：
| 项目 |
篮球 |
乒乓球 |
羽毛球 |
跳绳 |
其他 |
| 人数 |
a |
12 |
10 |
5 |
8 |
请根据图表中的信息完成下列各题：
（1）本次共调查学生名；
（2）a=，表格中五个数据的中位数是；
（3）在扇形图中，“跳绳”对应的扇形圆心角是°；
（4）如果该年级有450名学生，那么据此估计大约有人最喜欢“乒乓球”．
如图，在△ABC中，AB＝AC，D，E分别是AB，AC的中点.
（1）试说明BE＝CD；
（2）请用一句话叙述由第（1）小题得出的结论.
如图，正方形的边长为x，用代数式表示图中阴影部分的面积，并计算当
时，阴影部分的面积.（
取3.14）
已知函数图象如图所示，根据图象可得：
（1）抛物线顶点坐标；
（2）对称轴为；
（3）当x=时，y有最大值是；
（4）当时，y随着x得增大而增大。
（5）当时，y＞0.