(本小题满分10分)给定两个命题, :对任意实数
:对任意实数
 都有
都有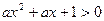 恒成立;
恒成立;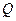 :关于
:关于 的方程
的方程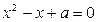 有实数根;如果
有实数根;如果 与
与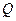 中有且仅有一个为真命题,求实数
中有且仅有一个为真命题,求实数 的取值范围.
的取值范围.
在等差数列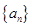 中,
中,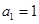 ,前
,前 项和
项和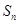 满足条件
满足条件 ,
,
(Ⅰ)求数列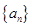 的通项公式;
的通项公式;
(Ⅱ)记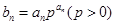 ,求数列
,求数列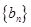 的前
的前 项和
项和 。
。
建造一间地面面积为12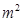 的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/
的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/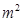 , 侧面的造价为80元/
, 侧面的造价为80元/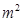 , 屋顶造价为1120元. 如果墙高3
, 屋顶造价为1120元. 如果墙高3 , 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元?
, 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元?
在△ABC中,角A、B、C所对应的边为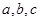
(1)若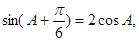 求A的值;
求A的值;
(2)若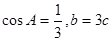 ,求
,求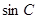 的值.
的值.
已知函数f(x)=3x2+bx+c,不等式f(x)>0的解集为(-∞,-2)∪(0,+∞).
(1) 求函数f(x)的解析式;
(2) 已知函数g(x)=f(x)+mx-2在(2,+∞)上单调增,求实数m的取值范围;
(3) 若对于任意的x∈[-2,2],f(x)+n≤3都成立,求实数n的最大值.
已知全集U={x | x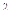 -7x+10≥0},A="{x" | |x -4| >2} ,B="{x" |
-7x+10≥0},A="{x" | |x -4| >2} ,B="{x" | 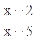 ≥0},
≥0},
求:C UA,A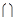 B
B