水库的蓄水量随时间而变化,现用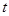 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于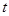 的近似函数关系式为:
的近似函数关系式为:
(1)该水库的蓄水量小于50的时期称为枯水期,以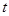 表示第
表示第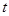 月份(
月份(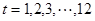 ),问:同一年内哪些月份是枯水期?
),问:同一年内哪些月份是枯水期?
(2)求一年内哪个月份该水库的蓄水量最大,并求最大蓄水量。(取 计算)
计算)
计算下列定积分(本小题满分12分)
(1)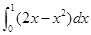 (2)
(2)
(3)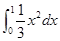 (4)
(4)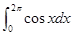
求下列函数的导数(本小题满分12分)
(1)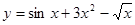 (2)
(2)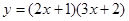
(3)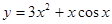 (4)
(4)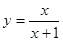
(本小题满分14分)
已知二次函数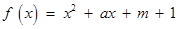 ,关于
,关于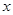 的不等式
的不等式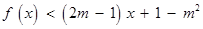 的解集为
的解集为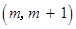 ,其中
,其中 为非零常数.设
为非零常数.设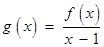 .
.
(1)求 的值;
的值;
(2) R
R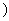 如何取值时,函数
如何取值时,函数

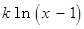 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若 ,且
,且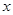
 ,求证:
,求证: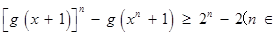 N
N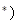
(本小题满分14分)
已知椭圆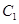 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为 ,
,
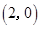 ,点
,点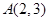 在椭圆
在椭圆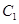 上,过点
上,过点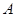 的直线
的直线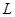 与抛物线
与抛物线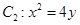 交于
交于 两点,抛物线
两点,抛物线 在点
在点 处的切线分别为
处的切线分别为 ,且
,且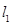 与
与 交于点
交于点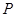 .
.
(1) 求椭圆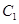 的方程;
的方程;
(2) 是否存在满足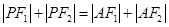 的点
的点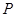 ? 若存在,指出这样的点
? 若存在,指出这样的点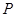 有几个(不必求出点
有几个(不必求出点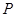 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
(本小题满分14分)
已知数列 的前
的前 项和为
项和为 ,且
,且  N
N .
.
(1) 求数列 的通项公式;
的通项公式;
(2)若 是三个互不相等的正整数,且
是三个互不相等的正整数,且 成等差数列,试判断
成等差数列,试判断 是否成等比数列?并说明理由.
是否成等比数列?并说明理由.