(本小题满分12分)已知方程 的系数a在[0,2]内取值,b在[0,3]内取值,求使方程没有实根的概率.
的系数a在[0,2]内取值,b在[0,3]内取值,求使方程没有实根的概率.
(本小题满分12分)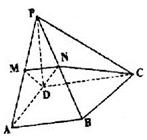
在四棱锥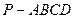 中,
中, ,
,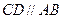 ,
,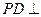 底面
底面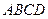 ,
,  ,直线
,直线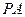 与底面
与底面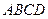 成
成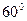 角,点
角,点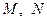 分别是
分别是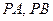 的中点.
的中点.
(1)求二面角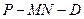 的大小;
的大小;
(2)当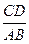 的值为多少时,
的值为多少时,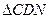 为直角三角形.
为直角三角形.
(本小题满分12分)
从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同。
(1)若抽取后又放回,抽3次,分别求恰2次为红球的概率及抽全三种颜色球的概率;
(2)若抽取后不放回,求抽完红球所需次数不少于4次的概率。
(本小题满分10分)
在 中,角
中,角 、
、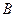 、
、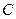 的对边分别为
的对边分别为 、
、 、
、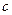 ,且
,且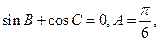
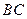 边上的中线
边上的中线 的长为
的长为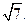
(I)求角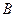 的大小;
的大小;
(II)求 的面积.
的面积.
已知函数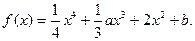
(1)若函数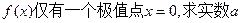 的取值范围;
的取值范围; (2)若对任意的
(2)若对任意的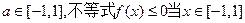 时恒成立,求实数b的取值范围。
时恒成立,求实数b的取值范围。
已知焦点在x轴上,离心率为 的椭圆的一个顶点是抛物线
的椭圆的一个顶点是抛物线 的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且
的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且

(1)求椭圆的方程;
(2)证明: 为定值。
为定值。