(本小题13分)
在正方体ABCD—A1B1C1D1中,M、N、G分别是A1A,D1C,AD的中点.
求证:(Ⅰ)MN//平面ABCD;(Ⅱ)MN⊥平面B1BG.
如图,在四棱锥 中,底面
中,底面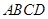 是
是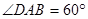 且边长为
且边长为 的菱形,侧面
的菱形,侧面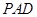 是等边三角形,且平面
是等边三角形,且平面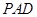 ⊥底面
⊥底面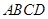 .
.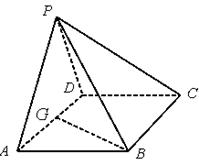
(1)若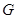 为
为 的中点,求证:
的中点,求证: 平面
平面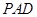 ;
;
(2)求证: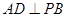 ;
;
(3)求二面角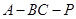 的大小.
的大小.
如图,在底面是直角梯形的四棱锥S-ABCD中,


(1)求四棱锥S-ABCD的体积;
(2)求证:
(3)求SC与底面ABCD所成角的正切值。
如图,在长方体ABCD—A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.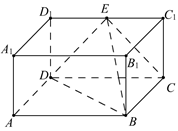
(1)求证:ED⊥平面EBC;
(2)求三棱锥E-DBC的体积.
在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点,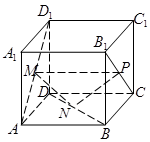
求证:(1)MN∥平面CC1D1D. (2)平面MNP∥平面CC1D1D.
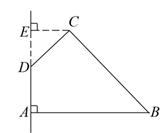
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.