(本小题12分)
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC—B.
(Ⅰ)试判断直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ)求直线BC与平面DEF所成角的余弦值;
(Ⅲ)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
(本小题满分13分)已知关于 的二次函数
的二次函数
(Ⅰ)设集合 和
和 ,分别从集合
,分别从集合 ,
,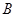 中随机取一个数作为
中随机取一个数作为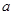 和
和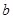 ,求函数
,求函数 在区间
在区间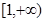 上是增函数的概率.
上是增函数的概率.
(Ⅱ)设点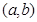 是区域
是区域 内的随机点,求函数
内的随机点,求函数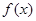 在区间
在区间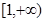 上是增函数的概率.
上是增函数的概率.
(本小题满分12分)如图,四棱锥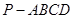 中,
中, 平面
平面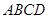 ,
, ,
,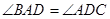
 ,
,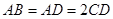 ,
,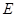 为
为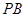 的中点.
的中点.
(Ⅰ)证明: ;
;
(Ⅱ)若二面角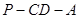 为
为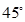 ,求直线
,求直线 与平面
与平面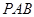 所成角的正切值.
所成角的正切值.
(Ⅲ)若 ,求平面
,求平面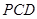 与平面PAB所成的锐二面角的余弦值
与平面PAB所成的锐二面角的余弦值
(本小题满分12分)为了分析某次考试数学成绩情况,用简单随机抽样从某班中抽取25名学生的成绩(百分制)作为样本,得到频率分布表如下:
| 分数 |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 频数 |
2 |
3 |
9 |
a |
1 |
| 频率 |
0.08 |
0.12 |
0.36 |
b |
0.04 |
(Ⅰ)求样本频率分布表中a,b的值,并根据上述频率分布表,在下表中作出样本频率分布直方图;
(Ⅱ)计算这25名学生的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)从成绩在[50,70)的学生中任选2人,求至少有1人的成绩在[60,70)中的概率.
(本小题满分12分)已知圆
 ,直线
,直线
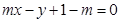 ,且直线
,且直线 与圆
与圆 相交于
相交于 ,
, 两点.
两点.
(Ⅰ)若 ,求直线
,求直线 的倾斜角;
的倾斜角;
(Ⅱ)若点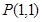 满足
满足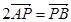 ,求此时直线
,求此时直线 的方程。
的方程。
(本小题满分12分)在一个盒子中装有6枝圆珠笔,其中3枝一等品,2枝二等品和1枝三等品,从中任取3枝,
求:(Ⅰ)取出的3枝中恰有1枝一等品的概率;
(Ⅱ)取出的3枝中一、二、三等品各一枝的概率;
(Ⅲ)取出的3枝中没有三等品的概率.