(本小题满分12分)在一个盒子中装有6枝圆珠笔,其中3枝一等品,2枝二等品和1枝三等品,从中任取3枝,
求:(Ⅰ)取出的3枝中恰有1枝一等品的概率;
(Ⅱ)取出的3枝中一、二、三等品各一枝的概率;
(Ⅲ)取出的3枝中没有三等品的概率.
已知点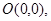

(1)是否存在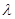 ,使得点P在第一、三象限的角平分线上?
,使得点P在第一、三象限的角平分线上?
(2)是否存在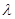 ,使得四边形
,使得四边形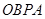 为平行四边形?(若存在,则求出
为平行四边形?(若存在,则求出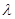 的值,若不存在,请说明理由.)
的值,若不存在,请说明理由.)
已知函数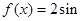
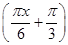
 ,点A、B分别是函数
,点A、B分别是函数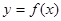 图像上的最高点和最低点.
图像上的最高点和最低点.
(1)求点A、B的坐标以及 ·
· 的值;
的值;
(2)设点A、B分别在角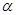 、
、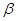 的终边上,求tan(
的终边上,求tan(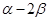 )的值.
)的值.
已知奇函数 f (x) 在 (-¥,0)∪(0,+¥) 上有意义,且在 (0,+¥) 上是增函数,f (1) = 0,又函数 g(q) = sin 2q+ m cos q-2m,若集合M =" {m" | g(q) < 0},集合 N =" {m" | f [g(q)] < 0},求M∩N.
已知点 是直线
是直线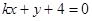
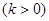 上一动点,
上一动点,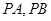 是圆C:
是圆C: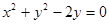 的两条切线,A、B是切点,若四边形
的两条切线,A、B是切点,若四边形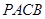 的最小面积是2,则
的最小面积是2,则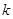 的值为?
的值为?
已知 ,函数
,函数 .
.
(1)求函数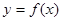 的周期和对称轴方程;
的周期和对称轴方程;
(2)求函数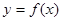 的单调递减区间.
的单调递减区间.