(本小题 满分14分)
满分14分)
已知 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 ,向量
,向量
 ,且
,且 .
.
(1)求角A的大小;
(2)若 ,试判断
,试判断 取得最大值时
取得最大值时 形状.
形状.
如图,在四棱锥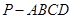 中,
中, 为
为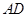 上一点,面
上一点,面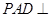 面
面 ,四边形
,四边形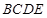 为矩形
为矩形 ,
, ,
,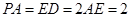 .
.
(1)已知 ,且
,且 ∥面
∥面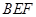 ,求
,求 的值;
的值;
(2)求证: 面
面 ,并求点
,并求点 到面
到面 的距离.
的距离.
已知等比数列 中,
中, ,前
,前 项和是前
项和是前 项中所有偶数项和的
项中所有偶数项和的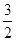 倍.
倍.
(1)求通项 ;
;
(2)已知 满足
满足 ,若
,若 是递增数列,求实数
是递增数列,求实数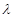 的取值范围.
的取值范围.
已知箱子里装有4张大小、形状都相同的卡片,标号分别为1,2,3,4.
(1)从箱子中任取两张卡片,求两张卡片的标号之和不小于5的概率;
(2)从箱子中任意取出一张卡片,记下它的标号 ,然后再放回箱子中;第二次再从箱子中任取一张卡片,记下它的标号
,然后再放回箱子中;第二次再从箱子中任取一张卡片,记下它的标号 ,求使得幂函数
,求使得幂函数 图像关于
图像关于 轴对称的概率.
轴对称的概率.
已知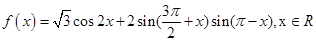
(1)最小正周期及对称轴方程;
(2)已知锐角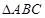 的内角
的内角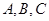 的对边分别为
的对边分别为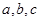 ,且
,且 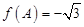 ,
,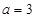 ,求
,求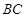 边上的高的最大值.
边上的高的最大值.
设 ,曲线
,曲线 在点
在点 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)求 的值;
的值;
(2)若对于任意的 ,
, 恒成立,求
恒成立,求 的范围;
的范围;
(3)求证: