附加题(本题满分10分)某厂生产某种零件,每个零件的成本为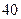元-优题课

题文

附加题(本题满分10分)
某厂生产某种零件,每个零件的成本为元,出厂单价定为元,该厂为鼓励销售部门订购,决定当一次订购量超过个时,每多订购一个，订购全部零件的出厂单价就降元,但实际出厂单价不能低于元．
（Ⅰ)当一次订购量为多少时，零件的实际出厂单价恰降为元？
（Ⅱ)当一次订购量为个，零件的实际出厂单价为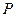元，写出函数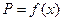的表达式.
（Ⅲ)当销售商一次订购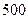个零件时,该厂获得的利润是多少元?如果订购个,利润是多少元?

科目数学题型解答题难度较易

登录免费查看答案和解析

相关试题

①．求函数的定义域；
②求函数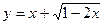的值域；
③求函数的值域.

已知一动圆M,恒过点F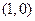，且总与直线相切．
（Ⅰ）求动圆圆心M的轨迹C的方程；
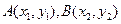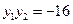（Ⅱ）探究在曲线C上,是否存在异于原点的两点,当时,
直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由．

设O是坐标原点,F是抛物线y²=2px(p＞0)的焦点,A是抛物线上的一个动点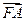，与
x轴正方向的夹角为60⁰,求|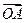|的值．

双曲线的中心为原点 $O$ ，焦点在 $x$ 轴上，两条渐近线分别为 $l_{1}, l_{2}$ ，经过右焦点 $F$ 垂直于 $l_{1}$ 的直线分别交 $l_{1}, l_{2}$ 于 $A, B$ 两点．已知 $|\vec{O A}|, |\vec{A B}|, |\vec{O B}|$ 成等差数列，且 $\vec{B F}$ 与 $\vec{F A}$ 同向．
（Ⅰ）求双曲线的离心率；
（Ⅱ）设 $A B$ 被双曲线所截得的线段的长为4，求双曲线的方程．

(本小题满分12分) 已知定义域为R的函数是奇函数．
(1) 求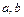的值；
(2)若对任意的, 不等式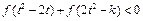恒成立, 求k的取值范围.

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号