双曲线的中心为原点
,焦点在
轴上,两条渐近线分别为
,经过右焦点
垂直于
的直线分别交
于
两点.已知
成等差数列,且
与
同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设
被双曲线所截得的线段的长为4,求双曲线的方程.
已知定点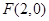 和定直线
和定直线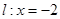 ,动点与定点
,动点与定点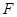 的距离等于点
的距离等于点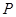 到定直线
到定直线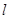 的距离,记动点
的距离,记动点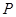 的轨迹为曲线
的轨迹为曲线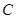 .
.
(1)求曲线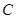 的方程.
的方程.
(2)若以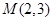 为圆心的圆与曲线
为圆心的圆与曲线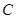 交于
交于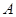 、
、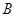 不同两点,且线段
不同两点,且线段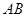 是此圆的直径时,求直线
是此圆的直径时,求直线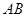 的方程.
的方程.
在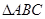 中,角
中,角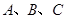 所对的边分别为
所对的边分别为 ,已知
,已知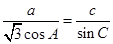 ,
,
(1)求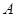 的大小;
的大小;
(2)若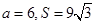 ,求
,求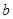 和
和 的值.
的值.
命题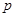 :方程
:方程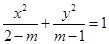 表示的曲线是焦点在y轴上的双曲线,命题
表示的曲线是焦点在y轴上的双曲线,命题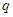 :方程
:方程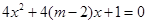 无实根,若
无实根,若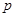 ∨
∨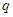 为真,
为真,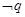 为真,求实数
为真,求实数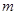 的取值范围.
的取值范围.
已知数列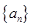 的前n项和
的前n项和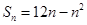
(1)求数列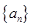 的通项公式,并证明
的通项公式,并证明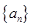 是等差数列;
是等差数列;
(2)若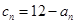 ,求数列
,求数列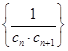 的前
的前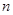 项和
项和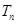 .
.
如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点, M为CD的中点.
M为CD的中点.
(1)求点M的轨迹方程;
(2)过M作AB的垂线,垂足为N,若存在正常数 ,使
,使 ,且P点到A、B 的距离和为定值,求点P的轨迹E的方程;
,且P点到A、B 的距离和为定值,求点P的轨迹E的方程;
(3)过 的直线与轨迹E交于P、Q两点,求
的直线与轨迹E交于P、Q两点,求 面积的最大值.
面积的最大值.