某商场“五一”期间举行有奖促销活动,顾客只要在商店购物满800元就能得到一次摸奖机会.摸奖规则是:在盒子内预先放有5个大小相同的球,其中一个球标号是0,两个球标号都是40,还有两个球没有标号。顾客依次从盒子里摸球,每次摸一个球(不放回),若累计摸到两个没有标号的球就停止摸球,否则将盒子内球摸完才停止.奖金数为摸出球的标号之和(单位:元),已知某顾客得到一次摸奖机会。
(1)求该顾客摸三次球被停止的概率;
(2)设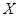 为该顾客摸球停止时所得的奖金数,求
为该顾客摸球停止时所得的奖金数,求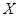 的分布列及均值.
的分布列及均值.
在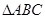 中,角
中,角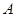 、
、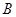 、
、 的对边分别为
的对边分别为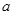 、
、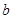 、
、 .已知
.已知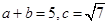 ,且
,且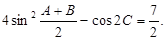
(1) 求角 的大小;
的大小;
(2)求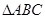 的面积
的面积
等比数列{an}的各项均为正数,且 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前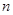 项和.
项和.
如果以数列 的任意连续三项作边长,都能构成一个三角形,那么称这样的数列
的任意连续三项作边长,都能构成一个三角形,那么称这样的数列 为“三角形”数列;又对于“三角形”数列
为“三角形”数列;又对于“三角形”数列 ,如果函数y=f(x)使得由
,如果函数y=f(x)使得由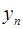 =f(
=f( )(
)(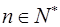 )确定的数列
)确定的数列 仍成为一个“三角形”数列,就称y="f(x)" 是数列
仍成为一个“三角形”数列,就称y="f(x)" 是数列 的“保三角形”函数。
的“保三角形”函数。
(Ⅰ)、已知数列 是首项为2012,公比为
是首项为2012,公比为 的等比数列,求证:
的等比数列,求证: 是“三角形”数列;
是“三角形”数列;
(Ⅱ)、已知数列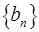 是首项为2,公差为1的等差数列,若函数f(x)=
是首项为2,公差为1的等差数列,若函数f(x)= (m>0且m≠1)是
(m>0且m≠1)是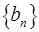 的“保三角形”函数. 求m的取值范围.
的“保三角形”函数. 求m的取值范围.
向量 =(4cos
=(4cos , sin
, sin ),
), 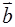 =(sin
=(sin , 4cos
, 4cos ),
), =(cos
=(cos , -4sin
, -4sin )(
)(
 且
且 、
、 均不等于
均不等于 ).
).
(Ⅰ)、求 的最大值;
的最大值;
(Ⅱ)、当 ∥
∥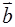 且
且  ⊥(
⊥(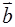 -2
-2 )时,求tan
)时,求tan + tan
+ tan 的值.
的值.