向量 =(4cos
=(4cos , sin
, sin ),
), 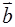 =(sin
=(sin , 4cos
, 4cos ),
), =(cos
=(cos , -4sin
, -4sin )(
)(
 且
且 、
、 均不等于
均不等于 ).
).
(Ⅰ)、求 的最大值;
的最大值;
(Ⅱ)、当 ∥
∥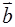 且
且  ⊥(
⊥(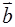 -2
-2 )时,求tan
)时,求tan + tan
+ tan 的值.
的值.
设函数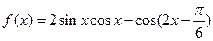 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当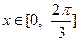 时,求函数
时,求函数 的最大值及取得最大值时的
的最大值及取得最大值时的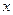 的值.
的值.
已知椭圆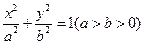 经过点
经过点 ,过右焦点F且不与x轴重合的动直线L交椭圆于
,过右焦点F且不与x轴重合的动直线L交椭圆于 两点,当动直线L的斜率为2时,坐标原点O到L的距离为
两点,当动直线L的斜率为2时,坐标原点O到L的距离为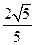 .
.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 过F的另一直线交椭圆于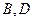 两点,且
两点,且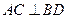 ,当四边形
,当四边形 的面积S=
的面积S=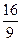 时,求直线L的方程.
时,求直线L的方程.
已知函数f(x)= 在x=-2处有极值.
在x=-2处有极值.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在区间[-3,3]上有且仅有一个零点,求b的取值范围.
已知数列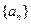 的前n项和为
的前n项和为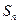 ,
, ,
,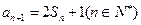 ,等差数列
,等差数列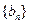 中
中
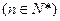 ,且
,且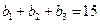 ,又
,又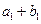 、
、 、
、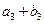 成等比数列.
成等比数列.
(Ⅰ)求数列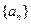 、
、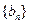 的通项公式;
的通项公式;
(Ⅱ)求数列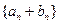 的前n项和Tn.
的前n项和Tn.
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为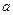 和
和 组成数对(
组成数对( ,并构成函数
,并构成函数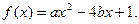
(Ⅰ)写出所有可能的数对( ,并计算
,并计算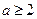 ,且
,且 的概率;
的概率;
(Ⅱ)求函数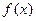 在区间[
在区间[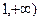 上是增函数的概率.
上是增函数的概率.