某商场“五一”期间举行有奖促销活动,顾客只要在商店购物满800元就能得到一次摸奖机会.摸奖规则是:在盒子内预先放有5个大小相同的球,其中一个球标号是0，两个球标号都是40，还有两个球没有标号。顾客依次从盒子里摸球，每次摸一个球（不放回），若累计摸到两个没有标号的球就停止摸球，否则将盒子内球摸完才停止.奖金数为摸出球的标号之和（单位：元），已知某顾客得到一次摸奖机会。
（1）求该顾客摸三次球被停止的概率；
（2）设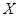
为该顾客摸球停止时所得的奖金数，求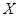的分布列及均值.
（本小题满分10分）等差数列
中，
，公差
且
成等比数列，前
项的和为
.
（1）求
及;
（2）设
，
，求
.
已知集合A＝{x|2≤x≤8}，B＝{x|1<x<6}，C＝{x|x>a}，U＝R.
（1）求A∪B，（∁UA）∩B；
（2）若A∩C≠∅，求a的取值范围．
证明：（1）对任一正整
，都存在整数
，使得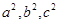
成等差数列。
（2）存在无穷多个互不相似的三角形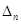
，其边长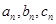
为正整数且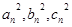
成等差数列。
已知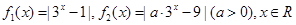
,
且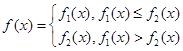
.
（Ⅰ）当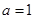
时,求
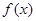在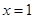
处的切线方程；
（Ⅱ）当
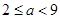时,设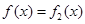
所对应的自变量取值区间的长度为
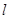（闭区间
的长度定义为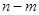
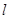）,试求的最大值；
（Ⅲ）是否存在这样的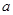
，使得当
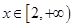时,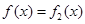?若存在,求出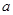的取值范围；若不存在，请说明理由.
已知椭圆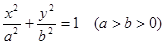
的离心率为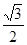
，椭圆的左、右两个顶点分别为
，
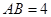，直线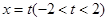
与椭圆相交于
两点，经过三点
的圆与经过三点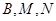
的圆分别记为圆C1与圆C2．
（1）求椭圆的方程；
（2）求证：无论
如何变化，圆C1与圆C2的圆心距是定值；
（3）当变化时，求圆C1与圆C2的面积的和
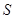的最小值．