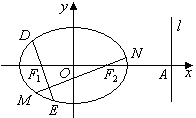某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
| 赔付金额(元) |
0 |
1000 |
2000 |
3000 |
4000 |
| 车辆数(辆) |
500 |
130 |
100 |
150 |
120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率;
(2)在样本车辆中,车主是新司机的占10℅,在赔付金额为4000元的样本车辆中,车主是新司机的占20℅,估计在已投保车辆中,新司机获赔金额为4000元的概率.
设 为正实数,
为正实数, ,
, ,
, 。
。
(Ⅰ)如果 ,则是否存在以
,则是否存在以 为三边长的三角形?请说明理由;
为三边长的三角形?请说明理由;
(Ⅱ)对任意的正实数 ,试探索当存在以
,试探索当存在以 为三边长的三角形时
为三边长的三角形时 的取值范围。
的取值范围。
已知 为坐标原点,
为坐标原点, ,
, 。
。
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)若 的定义域为
的定义域为 ,值域为
,值域为 ,求
,求 的值。
的值。
某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
| 版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
| 人数 |
20 |
15 |
5 |
10 |
(Ⅰ)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(Ⅱ)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
已知函数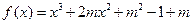 (其中
(其中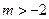 )
)
(1)若 ,求函数
,求函数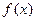 的单调区间及极小值;
的单调区间及极小值;
(2)若直线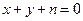 对任意的
对任意的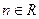 都不是曲线
都不是曲线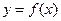 的切线,求
的切线,求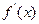 的最小值及实数
的最小值及实数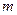 的取值范围.
的取值范围.
设椭圆 的焦点分别为
的焦点分别为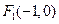 、
、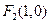 ,直线
,直线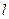 :
: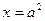 交
交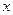 轴于点
轴于点 ,且
,且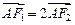 .
.
(1)试求椭圆的方程;
(2)过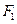 、
、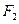 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于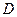 、
、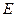 、
、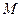 、
、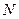 四点(如图所示),试求四边形
四点(如图所示),试求四边形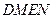 面积的最大值和最小值.
面积的最大值和最小值.