已知
分别是椭圆
的左、右焦点
关于直线
的对称点是圆
的一条直径的两个端点.
(Ⅰ)求圆
的方程;
(Ⅱ)设过点
的直线
被椭圆
和圆
所截得的弦长分别为
.当
最大时,求直线
的方程.
(本小题满分13分)已知函数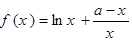 ,其中
,其中 为常数,且
为常数,且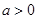 .
.
(1)若曲线 在点
在点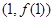 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;
(2)若函数 在区间
在区间 上的最小值为
上的最小值为 ,求
,求 的值.
的值.
(本大题13分)如图,已知椭圆 ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线 上.
上.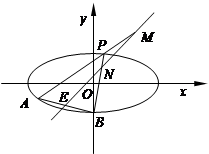
(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.
数列 ,
, ,
,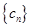 满足:
满足: ,
, ,
, .
.
(1)若数列 是等差数列,求证:数列
是等差数列,求证:数列 是等差数列;
是等差数列;
(2)若数列 ,
,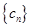 都是等差数列,求证:数列
都是等差数列,求证:数列 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列 是等差数列,试判断当
是等差数列,试判断当 时,数列
时,数列 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
(本小题满分12分)如图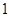 是图
是图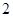 的三视图,三棱锥
的三视图,三棱锥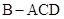 中,
中,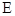 ,
,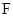 分别是棱
分别是棱 ,
,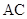 的中点.
的中点.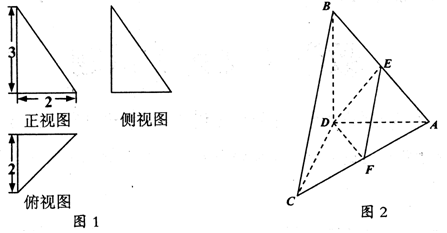
(1)求证: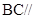 平面
平面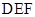 ;
;
(2)求三棱锥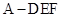 的体积.
的体积.
【原创】(本小题满分12分)已知在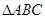 中,内角
中,内角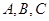 的对边分别是
的对边分别是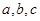 ,且
,且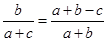 .
.
求角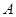 ;
;
若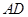 为
为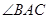 的平分线,
的平分线,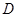 在边
在边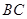 上,请用正弦定理证明:
上,请用正弦定理证明: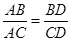 .
.