已知函数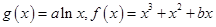 .
.
(1)若 在区间
在区间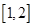 上不是单调函数,求实数
上不是单调函数,求实数 的范围;
的范围;
(2)若对任意 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当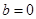 时,设
时,设 ,对任意给定的正实数
,对任意给定的正实数 ,曲线
,曲线 上是否存在两点
上是否存在两点 ,使得
,使得 是以
是以 (
( 为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在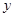 轴上?请说明利用.
轴上?请说明利用.
已知p:实数x满足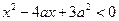 ,其中a<0;q:实数x满足
,其中a<0;q:实数x满足 且
且 的必要不充分条件,求a的范围.
的必要不充分条件,求a的范围.
如图,在长方体AC1中,AB=BC=2,AA1=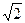 ,E.F分别是面A1C1.面BC1的中心,求(1)AF和BE所成的角.
,E.F分别是面A1C1.面BC1的中心,求(1)AF和BE所成的角.
(2)AA1与平面BEC1所成角的正弦值.
已知双曲线的中心在原点,焦点为F1 ,F2(0,
,F2(0,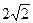 ),
),
且离心率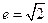 ,求双曲线的标准方程及其渐近线.
,求双曲线的标准方程及其渐近线.
生产某种商品x件,所需费用为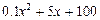 元,而售出x件这种商品时,每件的价格为p元,这里
元,而售出x件这种商品时,每件的价格为p元,这里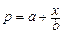 (a,b是常数)。
(a,b是常数)。
(1)写出出售这种商品所获得的利润y元与售出这种商品的件数x间的函数关系式;
(2)如果生产出来的这种商品都能卖完,那么当产品是150件时,所获得的利润最大,并且这时的价格是40元,求a,b的值。
已知定点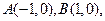 动点
动点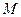 满足
满足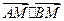 等于点
等于点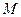 到
到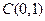 的距离平方的
的距离平方的 倍,试求动点
倍,试求动点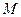 的轨迹方程,并说明方程所表示的曲线。
的轨迹方程,并说明方程所表示的曲线。