设
为数列{
}的前项和,已知
,2
(Ⅰ)求
,
,并求数列{
}的通项公式;
(Ⅱ)求数列{
}的前
项和。
某城市有连接8个小区A、B、C、D、E、F、G、H和市中心O的整齐方格形道路网,每个小方格均为正方形,如图,某人从道路网中随机地选择一条最短路径,由小区A前往H.
(1)列出此人从小区A到H的所有最短路径(自A至H依次用所经过的小区的字母表示);
(2)求他经过市中心O的概率.
斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥平面ABC,∠ACB=90°.
(1)求证:BC⊥AA1;
(2)若M,N是棱BC上的两个三等分点,求证:A1N∥平面AB1M.
已知函数f(x)=(x+2)|x-2|.
(1)若不等式f(x)≤a在[-3,1]上恒成立,求实数a的取值范围;
(2)解不等式f(x)>3x.
已知函数f(x)=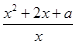 ,x∈[1,+∞),
,x∈[1,+∞),
(1)当a= 时,求函数f(x)的最小值.
时,求函数f(x)的最小值.
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
定义在R上的单调函数 满足
满足 且对任意
且对任意 都有
都有 .
.
(1)求证 为奇函数;
为奇函数;
(2)若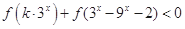 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.