某城市有连接8个小区A、B、C、D、E、F、G、H和市中心O的整齐方格形道路网，每个小方格均为正方形，如图，某人从道路网中随机地选择一条最短路径，由小区A前往H.
(1)列出此人从小区A到H的所有最短路径(自A至H依次用所经过的小区的字母表示)；
(2)求他经过市中心O的概率．
求下列函数f(x)的解析式．
(1) 已知f(1－x)＝2x2－x＋1，求f(x)；
(2) 已知f
＝x2＋
，求f(x)；
(3) 已知一次函数f(x)满足f(f(x))＝4x－1，求f(x)；
(4) 定义在(－1，1)内的函数f(x)满足2f(x)－f(－x)＝lg(x＋1)，求f(x)．
求下列各题中的函数f(x)的解析式．
(1) 已知f(
＋2)＝x＋4，求f(x)；
(2) 已知f
＝lgx，求f(x)；
(3) 已知函数y＝f(x)满足2f(x)＋f
＝2x，x∈R且x≠0，求f(x)；
(4) 已知f(x)是二次函数，且满足f(0)＝1，f(x＋1)＝f(x)＋2x，求f(x)．
判断下列对应是否是从集合A到集合B的函数．
(1) A＝B＝N*，对应法则f：x→y＝|x－3|，x∈A，y∈B；
(2) A＝[0，＋∞)，B＝R，对应法则f：x→y，这里y2＝x，x∈A，y∈B；
(3) A＝[1，8]，B＝[1，3]，对应法则f：x→y，这里y3＝x，x∈A，y∈B；
(4) A＝{(x，y)|x、y∈R}，B＝R，对应法则：对任意(x，y)∈A，(x，y)→z＝x＋3y，z∈B.
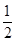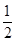已知数列{an}的前n项和Sn与通项an满足Sn=
-an.
(1)求数列{an}的通项公式;
(2)设f(x)=log3x,bn=f(a1)+f(a2)+…+f(an),Tn=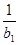
+
+…+
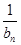,求T2012;
(3)若cn=an·f(an),求{cn}的前n项和Un.
已知等差数列{an}的首项为a,公差为d,且方程ax2-3x+2=0的解为1,d.
(1)求{an}的通项公式及前n项和公式;
(2)求数列{3n-1an}的前n项和Tn.