斜三棱柱ABC－A1B1C1中，侧面ACC1A1⊥平面ABC，∠ACB＝90°.
(1)求证：BC⊥AA1；
(2)若M，N是棱BC上的两个三等分点，求证：A1N∥平面AB1M.
已知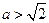
，求
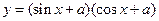的最值。
已知函数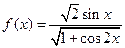
，
(1)求函数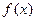
的定义域、值域、最小正周期；
(2)判断函数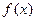奇偶性。
已知函数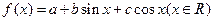
的图像过点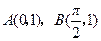
，且b>0，又
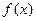的最大值为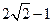
，(1)求函数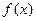的解析式；(2)由函数y=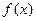图像经过平移是否能得到一个奇函数y=
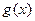的图像？若能，请写出平移的过程；若不能，请说明理由。
已知偶函数
的最小值为0，
求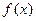
的最大值及此时x的集合。
对于函数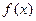
，若存在x0∈R，使f(x0)＝x0成立，则称x0为f(x)的不动点．如果函数f(x)＝
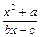有且仅有两个不动点0和2．
(Ⅰ)试求b、c满足的关系式；
(Ⅱ)若c＝2时，各项不为零的数列{an}满足4Sn·f(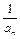
)＝1，
求证：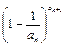
＜
＜
；
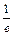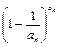(Ⅲ)设bn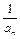＝－，Tn为数列{bn}的前n项和，求证：T2009－1＜ln2009＜T2008．