如图,两县城A和B相距20km,O为AB的中点,现要在以O为圆心、20km为半径的圆弧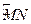 上选择一点P建造垃圾处理厂,其中
上选择一点P建造垃圾处理厂,其中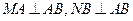 。已知垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A和城B的影响度之和。统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为9。记垃圾处理厂对城A和城B的总影响度为y,设AP=xkm,
。已知垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A和城B的影响度之和。统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为9。记垃圾处理厂对城A和城B的总影响度为y,设AP=xkm,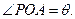
(I)写出x关于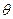 的函数关系,并求该函数的定义域和值域;
的函数关系,并求该函数的定义域和值域;
(II)当x为多少km时,总影响度最小?
(本小题满分12分)
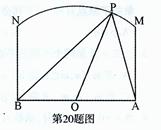
如图:在四棱锥 中,底面
中,底面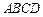 是菱形,
是菱形,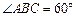 ,
,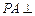 平面
平面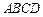 ,
,
点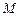 、
、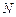 分别为
分别为 、
、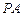 的中点,
的中点,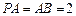 .
.
(I)证明: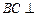 平面
平面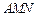 ;
;
(II)在线段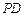 上是否存在一点
上是否存在一点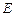 ,使得
,使得 平面
平面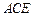 ;若存在,
;若存在, 求出
求出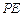 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
函数
(1)求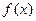 的周期;
的周期;
(2)若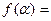
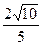 ,
,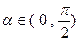 ,求
,求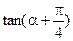 的值
的值
(本题满分14分)已知数列{an}的各项均为正数,观察右上方的程序框图,若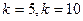 时,分别有
时,分别有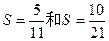
(1)试求数列{an}的通项;
(2)令 ,求数列
,求数列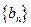 的前
的前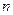 项和
项和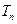 的值.
的值. 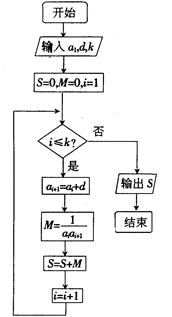
已知实数 ,设P:函数
,设P:函数 在R上单调递减,Q:关于
在R上单调递减,Q:关于 的一元二次方程
的一元二次方程 有两个不相等的实数根,如果命题“
有两个不相等的实数根,如果命题“ ”为真命题,命题“
”为真命题,命题“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
(本题满分14分) 假设关于某设备的使用年限 和所支出的维修费用
和所支出的维修费用 (万元)有如下的统计数据,由资料显示
(万元)有如下的统计数据,由资料显示 对
对 呈线性相关关系.
呈线性相关关系.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程。
(2)试根据(1)求出的线性回归方程,预测使用年限为10年时,维修费用是多少?