如图所示,直线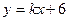 与
与 轴
轴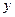 轴分别交于点E,
轴分别交于点E, F,点E的坐标为(-8,0),点A的坐标为(-6,0)。
F,点E的坐标为(-8,0),点A的坐标为(-6,0)。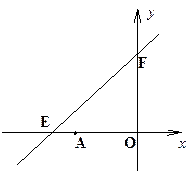
(1)求 的值;
的值;
(2)若点P(
 ,
,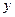 )是第二象限内的直线上的一个动点,当点P运动过程中,试写出△OPA的面积S与
)是第二象限内的直线上的一个动点,当点P运动过程中,试写出△OPA的面积S与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)当点P运动到什么位置时,△OPA的面积为 ?
?
(年四川南充8分)如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
(1)求证:直线EP为⊙O的切线;
(2)点P在劣弧AC上运动,其他条件不变,若BG2=BF•BO.试证明BG=PG;
(3)在满足(2)的条件下,已知⊙O的半径为3,sinB= .求弦CD的长.
.求弦CD的长.
(年山东莱芜10分)如图1,在⊙O中,E是弧AB的中点,C为⊙O上的一动点(C与E在AB异侧),连接EC交AB于点F,EB= (r是⊙O的半径).
(r是⊙O的半径).
(1)D为AB延长线上一点,若DC=DF,证明:直线DC与⊙O相切;
(2)求EF•EC的值;
(3)如图2,当F是AB的四等分点时,求EC的值.
(2014年山东济南9分)如图1,有一组平行线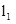 ∥
∥ ∥
∥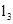 ∥
∥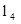 ,正方形ABCD的四个顶点分别在
,正方形ABCD的四个顶点分别在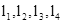 上,EG过点D且垂直于
上,EG过点D且垂直于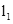 于点E,分别交
于点E,分别交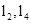 于点F,G,
于点F,G,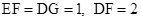 .
.
(1)AE= ,正方形ABCD的边长= ;
(2)如图2,将∠AEG绕点A顺时针旋转得到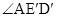 ,旋转角为
,旋转角为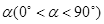 ,点
,点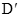 在直线
在直线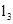 上,以
上,以 为边在的
为边在的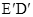 左侧作菱形
左侧作菱形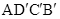 ,使点
,使点 分别在直线
分别在直线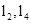 上.
上.
①写出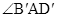 与
与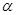 的函数关系并给出证明;
的函数关系并给出证明;
②若 ,求菱形
,求菱形 的边长.
的边长.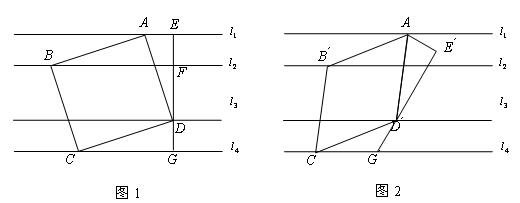
(年辽宁营口14分)四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;
(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.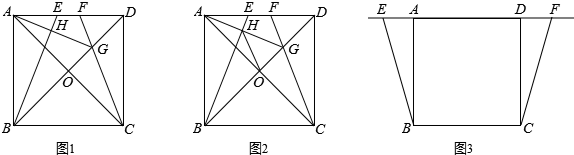
(年辽宁盘锦14分)已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.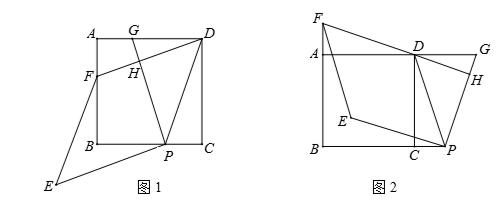
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.