(年辽宁盘锦14分)已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.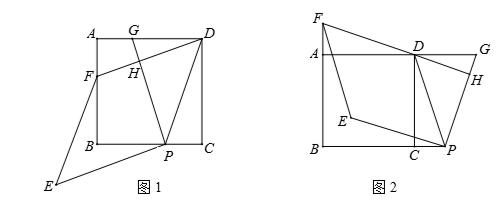
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.
为了扶持农民发展农业生产,国家对购买农机的农户给予农机售价13%的政府补贴.某市农机公司筹集到资金130万元,用于一次性购进A、B两种型号的收割机共30台(购机费用不超过筹集资金).根据市场需求,这些收割机可以全部销售,全部销售后利润不少于15万元.其中,收割机的进价和售价见下表:
| A型收割机 |
B型收割机 |
|
| 进价(万元/台) |
5.3 |
3.6 |
| 售价(万元/台) |
6 |
4 |
设公司计划购进A型收割机x台,收割机全部销售后公司获得的利润为y万元.
(1)试写出y与x的函数关系式;
(2)市农机公司有哪几种购进收割机的方案可供选择?
(3)选择哪种购进收割机的方案,农机公司获利最大?最大利润是多少?此种情况下,购买这30台收割机的所有农户获得的政府补贴总额W为多少万元?
 在“传箴言”活动中,某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计,并制成了如下两幅不完整的统计图:
在“传箴言”活动中,某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计,并制成了如下两幅不完整的统计图:
(1)求该班团员在这一个月内所发箴言的平均条数是多少?并将该条形统计图补充完整;
(2)如果发了3条箴言的同学中有两位男同学,发了4条箴言的同学中有三位女同学.现要从发了3条箴言和4条箴言的同学中分别选出一位参加该校团委组织的“箴言”活动总结会,请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
已知:如图,在平面直角坐标系xOy中,直线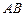 与
与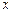 轴交于点A (– 2,0),与反比例函数在第一象限内的图象交于点B (2,n),连结BO,若
轴交于点A (– 2,0),与反比例函数在第一象限内的图象交于点B (2,n),连结BO,若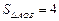 .
.
(1)求该反比例函数的解析式和直线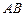 的解析式;
的解析式;
(2)若直线AB与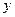 轴的交点为C,求△OCB的面积.
轴的交点为C,求△OCB的面积.
先化简,再求值: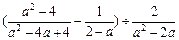 ,其中
,其中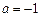 .
.
如图所示,
A、B两城市相距100 km,现计划在这两座城市间修建一条高速公路(即线段AB),经 测量,森林保护中心P在A城市的北偏东
测量,森林保护中心P在A城市的北偏东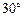 和B城市的北偏西
和B城市的北偏西 的方向上,已知森林保护区的范围在以P点为圆心,50 km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:
的方向上,已知森林保护区的范围在以P点为圆心,50 km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据: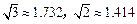 )
)