（本小题满分12分）如图，在平面直角坐标系xOy中，若点A（－2，n），B（1，－2）是一次函数y=kx+b的图象和反比例函数y=
的图象的两个交点．
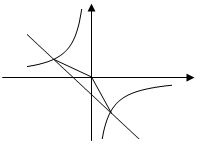
（1）求反比例函数和一次函数的解析式；
（2）求直线AB与x轴的交点C的坐标；
（3）求点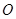
到直线AB的距离．
(本题满分8分) 已知a是一元二次方程x2－4x+1=0的两个实数根中较小的根，
①求a2-4a+2012的值
② 化简求值
为落实国务院房地产调控政策，使“居者有其屋”，某市加快了廉租房的建设力度．2010年市政府共投资2亿元人民币建设了廉租房8万平方米，预计到2012年底三年共累计投资9.5亿元人民币建设廉租房，若在这两年内每年投资的增长率相同．
(1)求每年市政府投资的增长率；
(2)若这两年内的建设成本不变，求到2012年底共建设了多少万平方米廉租房
如图，在梯形ABCD中，AD∥BC，∠B=90°，∠C=45°，AD=1，BC=4，E为AB中点，EF∥DC交BC于点F，求EF的长．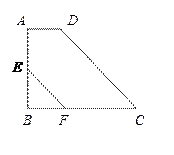
已知：关于x的一元二次方程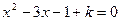
有两个不相等的实数根．
（1）求k的取值范围；
（2）请选择一个k的正整数值，并求出方程的根．
(本题满分8分)
已知：如图,四边形ABCD是平行四边形,△ADE和△BCF都是
等边三角形.
求证:BD和EF互相平分. 