某市记者为了调查该市市民对雾霾天气成因的认识情况,进行了随机调查,并对结果绘制成如下不完整的统计图表.
| 组别 |
观点 |
频数 |
| A |
大气气压低,空气不流动 |
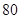 |
| B |
地面灰尘大,空气湿度低 |
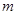 |
| C |
汽车尾气排放 |
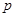 |
| D |
工厂造成的污染 |
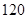 |
| E |
其他 |
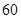 |
请根据图表中提供的信息解答下列问题:
(1)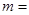 ,
,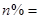
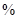 ;
;
(2)若该市人口约为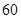 万人,请你估计其中持
万人,请你估计其中持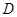 组“观点”的市民人数;
组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,抽中持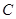 组“观点”的人概率是多少?
组“观点”的人概率是多少?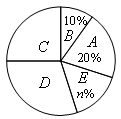
先化简,再求值: ,然后从 ,0,1中选择适当的数代入求值.
如图1,平面直角坐标系 中,等腰 的底边 在 轴上, ,顶点 在 的正半轴上, ,一动点 从 出发,以每秒1个单位的速度沿 向左运动,到达 的中点停止.另一动点 从点 出发,以相同的速度沿 向左运动,到达点 停止.已知点 、 同时出发,以 为边作正方形 ,使正方形 和 在 的同侧,设运动的时间为 秒 .
(1)当点 落在 边上时,求 的值;
(2)设正方形 与 重叠面积为 ,请问是否存在 值,使得 ?若存在,求出 值;若不存在,请说明理由;
(3)如图2,取 的中点 ,连结 ,当点 、 开始运动时,点 从点 出发,以每秒 个单位的速度沿 运动,到达点 停止运动.请问在点 的整个运动过程中,点 可能在正方形 内(含边界)吗?如果可能,求出点 在正方形 内(含边界)的时长;若不可能,请说明理由.

在平面直角坐标系 中,关于 的二次函数 的图象过点 , .
(1)求这个二次函数的表达式;
(2)求当 时, 的最大值与最小值的差;
(3)一次函数 的图象与二次函数 的图象交点的横坐标分别是 和 ,且 ,求 的取值范围.

如图,在 中, , 平分 交 于点 ,过点 和点 的圆,圆心 在线段 上, 交 于点 ,交 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)若 , ,求 的长.

小华同学将笔记本电脑水平放置在桌子上,当显示屏的边缘线 与底板的边缘线 所在水平线的夹角为 时,感觉最舒适(如图① .侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点 、 、 在同一直线上, , , .

(1)求 的长;
(2)如图④,垫入散热架后,要使显示屏的边缘线 与水平线的夹角仍保持 ,求点 到 的距离.(结果保留根号)