(本小题满分14分 )如图,棱锥
)如图,棱锥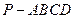 的底面
的底面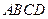 是矩形,
是矩形,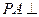 面
面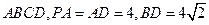 ,
,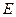 为
为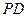 的中点.
的中点.
(1)求证: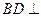 面
面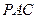 ;
;
(2)求二面角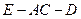 的余弦值;
的余弦值;
(3)设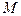 为
为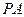 的中点,在棱
的中点,在棱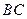 上是否存在点
上是否存在点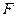 ,
,
使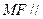 面
面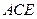 ?如果存在,请指出
?如果存在,请指出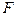 点的位置;
点的位置;
如果不存在,请说明理由.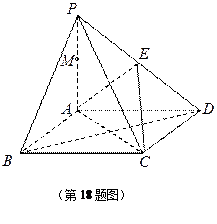
设椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 、
、 ,上顶点为
,上顶点为 ,在
,在 轴负半轴上有一点
轴负半轴上有一点 ,满足
,满足 ,且
,且 ⊥
⊥ .
.
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)若过 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(Ⅲ)在(Ⅱ)的条件下,过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆
与椭圆 交于
交于 、
、 两点,
两点,
若点 使得以
使得以 为邻边的平行四边形是菱形,求
为邻边的平行四边形是菱形,求 的取值范围.
的取值范围.
已知正△ 的边长为4,
的边长为4, 是
是 边上的高,
边上的高, 分别是
分别是 和
和 边的中点,现将△
边的中点,现将△ 沿
沿 翻折成直二面角
翻折成直二面角 ,如图.
,如图.
(I)证明: ∥平面
∥平面 ;
;
(II)求二面角 的余弦值;
的余弦值;
(Ⅲ)在线段 上是否存在一点
上是否存在一点 ,使
,使 ?证明你的结论.
?证明你的结论.
已知函数 ,
, .
.
(I)若函数 在
在 处取得极值,求
处取得极值,求 的单调区间;
的单调区间;
(II)当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知 .
.
(Ⅰ)若向量 ,
, ,且
,且 ∥
∥ ,求
,求 的值;
的值;
(Ⅱ)在 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进行第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品的合格率依次为 ,
, ,
, .经过第二次烧制后,甲、乙、丙三件产品的合格率均为
.经过第二次烧制后,甲、乙、丙三件产品的合格率均为 .
.
(Ⅰ)求第一次烧制后恰有一件产品合格的概率;
(Ⅱ)求经过前后两次烧制后三件产品均合格的概率.