给出下列四个命题:①命题“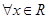 ,都有
,都有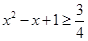 ”的否定是“
”的否定是“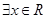 ,使
,使 ”②命题“设向量
”②命题“设向量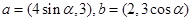 ,若
,若 ,则
,则 ”的逆命题、否命题、逆否命题中真命题的个数为2;③集合
”的逆命题、否命题、逆否命题中真命题的个数为2;③集合 ,
, ,则
,则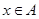 是
是 的充分不必要条件。
的充分不必要条件。
其中正确命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
把70个面包分5份给5个人,使每人所得成等差数列,且使较大的三份之和的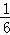 是较小的两份之和,问最小的1份为.()
是较小的两份之和,问最小的1份为.()
| A.2 | B.8 | C.14 | D.20 |
定义:在数列{an}中,若满足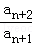 ﹣
﹣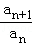 =d(n∈N+,d 为常数),称{an}为“等差比数列”.已知在“等差比数列”{an}中,a1=a2=1,a3=3,则
=d(n∈N+,d 为常数),称{an}为“等差比数列”.已知在“等差比数列”{an}中,a1=a2=1,a3=3,则 =()
=()
| A.4×20122﹣1 | B.4×20132﹣1 | C.4×20142﹣1 | D.4×20132 |
在圆x2+y2﹣5y=0内,过点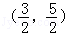 作n条弦(n∈N+),它们的长构成等差数列{an},若a1为过该点最短的弦,an为过该点最长的弦,且公差
作n条弦(n∈N+),它们的长构成等差数列{an},若a1为过该点最短的弦,an为过该点最长的弦,且公差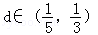 ,则n的值为()
,则n的值为()
| A.4 | B.5 | C.6 | D.7 |
已知数列{an}是各项均为正数且公比不等于1的等比数列.对于函数y=f(x),若数列{lnf(an)}为等差数列,则称函数f(x)为“保比差数列函数”.现有定义在(0,+∞)上的如下函数:
① ,
,
②f(x)=x2,
③f(x)=ex,
④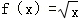 ,
,
则为“保比差数列函数”的所有序号为()
| A.①② | B.③④ | C.①②④ | D.②③④ |
对于各项均为整数的数列{an},如果ai+i(i=1,2,3,…)为完全平方数,则称数列{an}具有“P性质”,如果数列{an}不具有“P性质”,只要存在与{an}不是同一数列的{bn},且{bn}同时满足下面两个条件:①b1,b2,b3,…bn是a1,a2,a3,…,an的一个排列;②数列{bn}具有“P性质”,则称数列{an}具有“变换P性质”,下面三个数列:①数列1,2,3,4,5;②数列1,2,3,…,11,12;③数列{an}的前n项和为Sn= (n2﹣1).其中具有“P性质”或“变换P性质”的有()
(n2﹣1).其中具有“P性质”或“变换P性质”的有()
| A.③ | B.①③ | C.①② | D.①②③ |