（本小题满分14分）
现有甲、乙两个盒子，甲盒中装有4个白球和4个红球，乙盒中装有3个白球和若干个红球，若从乙盒中任取两个球，取到同色球的概率是
.
（1）求乙盒中红球的个数；
（2）从甲、乙两个盒子中各任取两个球进行交换，若交换后乙盒子中的白球数和红球数相等，就说这次交换是成功的，试求交换成功的概率。
（3
）若从甲盒中任取两个球，放入乙盒中均匀后，再从乙盒中任意取出2个球放回到甲盒中，求甲盒中白球没有增加的概率；
已知对任意的平面向量，把
绕其起点沿逆时针方向旋转
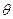角，得到向量
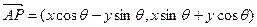，叫做把点B绕点A逆时针方向旋转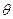角得到点P
①已知平面内的点A（1，2），B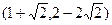
，把点B绕点A沿逆时针方向旋转
后得到点P，求点P的坐标
②设平面内曲线C上的每一点绕逆时针方向旋转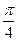
后得到的点的轨迹是曲线
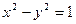，求原来曲线C的方程.
（本小题满分14分）设椭圆的中心是坐标原点，长轴在x轴上，离心率e=
，已知点P（0，
）到这个椭圆上的点的最远距离是
，求这个椭圆的方程。
（本小题满分12分）空间四边形OABC各边以及AC，BO的长都是1，点D，E分
别是边OA，BC的中点，连接DE
（1）求DE的长
（2）求证OA
BC
(本小题满分12分)
在
中，
，
，
.
（Ⅰ）求
的值；（Ⅱ）求
的值.
已知函数
（
）．
（1）当
时，
，且
为
上的奇函数．求
时的表达式；
（2）若
为偶函数，求
的值；
（3）对（2）中的函数
，设
，若函数
与
的图象有且只有一个公共点，求实数
的取值范围．