已知函数 (
( ).
).
(1)当 时,
时, ,且
,且 为
为 上的奇函数.求
上的奇函数.求 时
时 的表达式;
的表达式;
(2)若 为偶函数,求
为偶函数,求 的值;
的值;
(3)对(2)中的函数 ,设
,设 ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围.
的取值范围.
设不等式组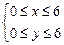 表示的区域为A,不等式组
表示的区域为A,不等式组 表示的区域为B,在区域A中任意取一点P
表示的区域为B,在区域A中任意取一点P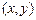 .
.
(Ⅰ)求点P落在区域B中的概率;
(Ⅱ)若 分别表示甲、乙两人各掷一次正方体骰子所得的点数,求点P落在区域B中的概率.
分别表示甲、乙两人各掷一次正方体骰子所得的点数,求点P落在区域B中的概率.
已知圆 经过
经过 和直线
和直线 相切,且圆心在直线
相切,且圆心在直线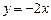 上.
上.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)若直线 经过圆
经过圆 内一点
内一点 与圆
与圆 相交于
相交于 两点,当弦
两点,当弦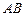 被点
被点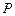 平分时,求直线
平分时,求直线 的方程
的方程
某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200 m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如ΔDQH等)上铺草坪,造价为80元/m2。
设总造价为S元,AD长为xm,试建立S与x的函数关系;
当x为何值时,S最小?并求这个最小值。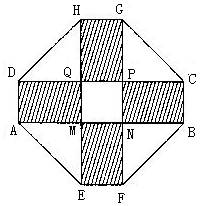
已知:在函数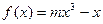 的图象上,以
的图象上,以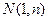 为切点的切线的倾斜角为
为切点的切线的倾斜角为
(I)求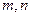 的值;
的值;
(II)是否存在最小的正整数 ,使得不等式
,使得不等式 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数 ,如果不存在,请说明理由。
,如果不存在,请说明理由。
直角坐标系中,O为坐标原点,设直线 经过点
经过点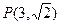 ,且与
,且与 轴交于
轴交于
点F(2,0)。
(I)求直线 的方程;
的方程;
(II)如果一个椭圆经过点P,且以点F为它的一个焦点,求椭圆的标准方程。