(本小题满分12分)
某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
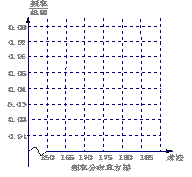
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
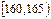 |
5 |
0.050 |
| 第2组 |
 |
① |
0.350 |
| 第3组 |
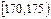 |
30 |
② |
| 第4组 |
 |
20 |
0.200 |
| 第5组 |
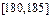 |
10 |
0.100 |
| 合计 |
100 |
1.00 |
已知 ,对
,对 :
: 和
和 是方程
是方程 的两个根,不等式
的两个根,不等式 对任意实数
对任意实数 恒成立;
恒成立; :函数
:函数 有两个零点,求使“
有两个零点,求使“ 且
且 ”为真命题的实数的取值范围。
”为真命题的实数的取值范围。
如图,某小区准备在一直角围墙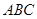 内的空地上植造“绿地
内的空地上植造“绿地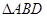 ”,其中
”,其中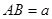 ,
,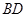 长可根据需要进行调节(
长可根据需要进行调节(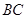 足够长),现规划在
足够长),现规划在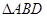 内接正方形
内接正方形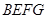 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积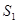 与种花的面积
与种花的面积 的比
的比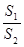 为
为 ,
,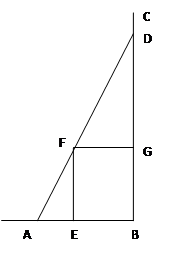
(1)设角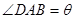 ,将
,将 表示成
表示成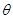 的函数关系;
的函数关系;
(2)当 为多长时,
为多长时, 有最小值,最小值是多少?
有最小值,最小值是多少?
正四棱锥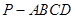 中,
中,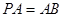 ,点M,N分别在PA,BD上,且
,点M,N分别在PA,BD上,且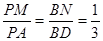 .
.
(Ⅰ)求异面直线MN与AD所成角;
(Ⅱ)求证: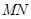 ∥平面PBC;
∥平面PBC;
(Ⅲ)求MN与平面PAB所成角的正弦值.
已知圆C的半径为2,圆心在x轴的正半轴上,直线 与圆C相切.
与圆C相切.
(I)求圆C的方程;
(II)过点Q(0,-3)的直线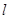 与圆C交于不同的两点A
与圆C交于不同的两点A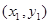 、B
、B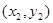 ,当
,当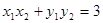 时,求△AOB的面积.
时,求△AOB的面积.
已知向量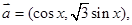
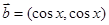 ,函数
,函数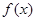

(Ⅰ)求函数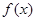 在
在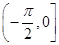 上的值域;
上的值域;
(Ⅱ)当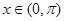 时,若
时,若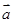 与
与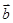 共线,求
共线,求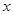 的值.
的值.