(本小题满分1 3分)如图6,正方形
3分)如图6,正方形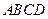 所在平面与圆
所在平面与圆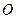 所在平面相交于
所在平面相交于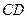 ,
,
线段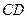 为圆
为圆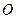 的弦,
的弦,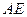 垂直于圆
垂直于圆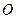 所在平面,
所在平面,
垂足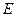 是圆
是圆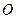 上异于
上异于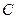 、
、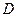 的点,
的点,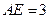 ,圆
,圆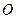 的直径为9.
的直径为9.
(1)求证:平面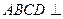 平面
平面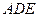 ;
;
(2)求二面角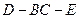 的平面角的正切值.
的平面角的正切值.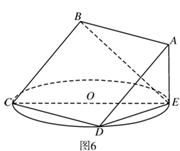
已知等差数列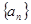 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项的和为
项的和为 ,且
,且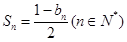 .
.
(1)求数列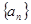 ,
, 的通项公式;
的通项公式;
(2)记 ,求证:
,求证: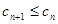 ;
;
(3)求数列 的前
的前 项和
项和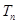 .
.
过点Q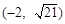 作圆C:
作圆C: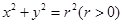 的切线,切点为D,且QD=4.
的切线,切点为D,且QD=4.
(1)求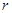 的值;
的值;
(2)设P是圆C上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y轴于点B,设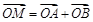 ,求
,求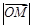 的最小值(O为坐标原点).
的最小值(O为坐标原点).
12分)某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.
已知如图:平行四边形ABCD中,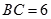 ,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.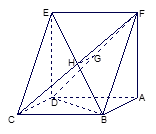
(1)求证:GH∥平面CDE;
(2)若 ,求四棱锥F-ABCD的体积.
,求四棱锥F-ABCD的体积.
设函数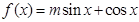
 的图象经过点
的图象经过点 .
.
(1)求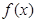 的解析式,并求函数的最小正周期.
的解析式,并求函数的最小正周期.
(2)若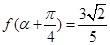 且
且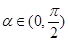 ,求
,求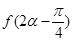 的值。
的值。