甲、乙两班参加植树活
动．乙班先植树30棵，然后甲班才开始与乙班一起植树．设甲班植树的总量为
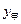（棵），乙班植树的总量为
（棵），两班一起植树所用的时间（从甲班开始植树时计时）为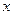
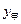（时），、分别与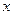之间的部分函数图象如图9
所示．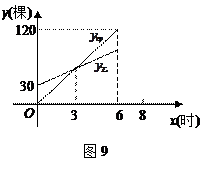
（1）当0≤x≤6时，分别求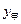、与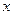之间的函数关系式；
（2）如果甲、乙两班均保持前6个小时的工作效率，通过计算说明，当
时，甲、乙两班植树的总量之和能否超过
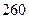棵．
先化简，再求值：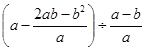
，其中a=sin30°，b=tan45°
如图(1)，直线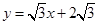
与x轴交于点A、与y轴交于点D，以AD为腰，以x轴为底作等腰梯形ABCD(AB＞CD)，且等腰梯形的面积是8
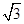，抛物线经过等腰梯形的四个顶点.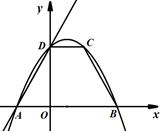
图(1)
(1) 求抛物线的解析式；
(2) 如图（2）若点P为BC上的—个动点（与B、C不重合），以P为圆心，BP长为半径作圆，与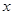
轴的另一个交点为E，作EF⊥AD，垂足为F，请判断EF与⊙P的位置关系，并给以证明；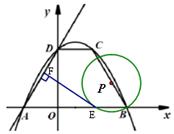
图（2）
(3) 在（2）的条件下，是否存在点P，使⊙P与y轴相切，如果存在，请求出点P的坐标；如果不存在，请说明理由.
如图，在△ABC中，已知AB=BC=AC=4cm，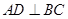
于D，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s，点Q沿CA，AB向终点B运动，速度为2cm/s，设它们运动的时间为t(s)，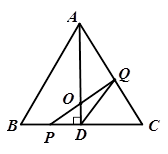
（1）求t为何值时，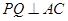
；
（2）当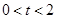
时，求证：AD平分△PQD的面积；
（3）当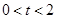时，求△PQD面积的最大值.
如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为直角边作等腰三角形CDE，其中∠DCE=90°，连接BE.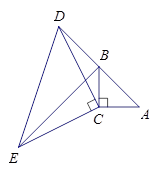
（1）求证：△ACD≌△BCE；
（2）若AC=3cm，求DE的长.
莲花山公园管理处计划购买甲、乙两种花木共6000株，甲种花木每株0.5元，乙种花木每株0.8元．相关资料表明：甲、乙两种花木的成活率分别为90%和95%．
（1）若购买这批花木共用了3600元，求甲、乙两种花木各购买了多少株？
（2）若要使这批花木的成活率不低于93%，且购买花木的总费用最低，应如何选购花木？