莲花山公园管理处计划购买甲、乙两种花木共6000株,甲种花木每株0.5元,乙种花木每株0.8元.相关资料表明:甲、乙两种花木的成活率分别为90%和95%.
(1)若购买这批花木共用了3600元,求甲、乙两种花木各购买了多少株?
(2)若要使这批花木的成活率不低于93%,且购买花木的总费用最低,应如何选购花木?
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.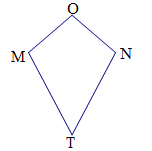
(1)试探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD,AC为对角线,BD=8.
①是否存在一个圆使得A,B,C,D四个点都在这个圆上?若存在,求出圆的半径;若不存在, 请说明理由;
②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE.当四边形ABED为菱形时,求点F到AB 的距离.
某校为了丰富学生的第二课堂,对学生参与演讲、舞蹈、书法和摄影活动的兴趣情况进行调查,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中最感兴趣的一项),对调查结果进行统计后,绘制了如下两个统计图:
(1)此次调查抽取的学生人数m= 名,其中选择“书法”的学生占抽样人数的百分比n= ;
(2)若该校有3000名学生,请根据以上数据估计该校对“书法”最感兴趣的学生人数.
如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)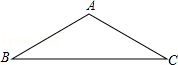
如图,在平行四边形ABCD中,AB<BC.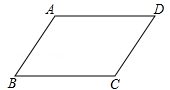
(1)利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则CE= .
(为方便答题,可在答题卡上画出你认为必要的图形)
在Rt△ABC中,∠A=90°,AC =" AB" = 4,D,E分别是边AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰RtRt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.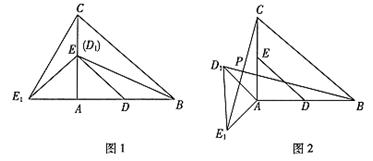
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1 = CE1 ,且BD1⊥ CE1 ;
(3)求点P到AB所在直线的距离的最大值.(直接写出结果)