已知函数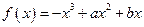 在区间
在区间 内,当
内,当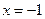 时取得极小值,当
时取得极小值,当 时取得极大值。
时取得极大值。
(1)求函数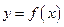 在
在 时的对应点的切线方程。
时的对应点的切线方程。
(2)求函数 在
在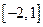 上的最大值与最小值。
上的最大值与最小值。
某人上午7:00乘汽车以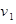 千米/小时
千米/小时 匀速从A地出发到距300公里的B地,在B地不作停留,然后骑摩托车以
匀速从A地出发到距300公里的B地,在B地不作停留,然后骑摩托车以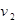 千米/小时
千米/小时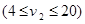 匀速从B地出发到距50公里的C地,计划在当天16:00至21:00到达C地。设乘汽车、骑摩托车的时间分别是x,y小时,如果已知所需的经费
匀速从B地出发到距50公里的C地,计划在当天16:00至21:00到达C地。设乘汽车、骑摩托车的时间分别是x,y小时,如果已知所需的经费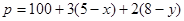 元,那么
元,那么 分别是多少时走的最经济,此时花费多少元?
分别是多少时走的最经济,此时花费多少元?
(本小题满分12分)在数列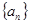 中,
中,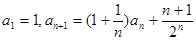
(1)设 求数列
求数列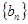 的通项公式;
的通项公式;
(2)求数列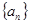 的前
的前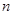 项和
项和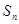 。
。
在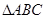 中,角
中,角 所对的边分别为
所对的边分别为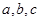 且满足
且满足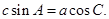
(1)求角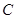 的大小;
的大小;
(2)求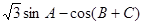 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角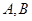 的大小.
的大小.
在△ABC中,角 的对应边分别是
的对应边分别是 满
满 .
.
(1)求角 的大小;
的大小;
(2)已知等差数列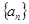 的公差不为零,若
的公差不为零,若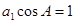 ,且
,且 成等比数列,求
成等比数列,求 的前
的前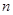 项和
项和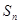 .
.
(本小题满分12分)已知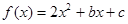 ,不等式
,不等式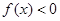 的解集是
的解集是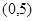 ,
,
(1)求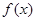 的解析式;
的解析式;
(2)若对于任意 ,不等式
,不等式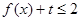 恒成立,求
恒成立,求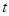 的取值范围.
的取值范围.