如图3所示的三角形数阵叫“莱布尼兹调和三角形”,
它们是由整数的倒数组成的,第 行有
行有 个数且两端的数均为
个数且两端的数均为
 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如 ,
, ,
, ,…,则第7行第4个数(从左往右数)为( )
,…,则第7行第4个数(从左往右数)为( )
A.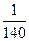 |
B. |
C. |
D. |
已知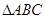 △ABC中,
△ABC中,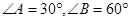 ,求证:
,求证: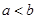 .证明:
.证明: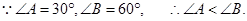 ∴
∴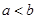 ,其中,画线部分是演绎推理的()
,其中,画线部分是演绎推理的()
| A.小前提 | B.大前提 | C.结论 | D.三段论 |
如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为()
| A.85,84 | B.84,85 | C.86,84 | D.84,84 |
设 (
( 是虚数单位),则复数
是虚数单位),则复数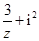 的实部是()
的实部是()
A. |
B. |
C.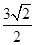 |
D. |
观察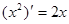 ,
,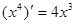 ,
,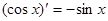 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在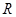 上的函数
上的函数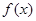 满足
满足 ,记
,记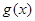 为
为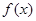 的导函数,则
的导函数,则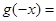 ()
()
A.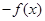 |
B.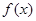 |
C.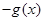 |
D.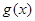 |
如图所示是《函数的应用》的知识结构图,如果要加入“用二分法求方程的近似解”,则应该放在()
| A.“函数与方程”的上位 | B.“函数与方程”的下位 |
| C.“函数模型及其应用”的上位 | D.“函数模型及其应用”的下位 |