如图所示是《函数的应用》的知识结构图,如果要加入“用二分法求方程的近似解”,则应该放在( )
| A.“函数与方程”的上位 | B.“函数与方程”的下位 |
| C.“函数模型及其应用”的上位 | D.“函数模型及其应用”的下位 |
下列说法:
(1)命题“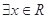 ,使得
,使得 ”的否定是“
”的否定是“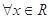 ,使得
,使得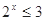 ”
”
(2)命题“函数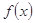 在
在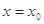 处有极值,则
处有极值,则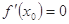 ”的否命题是真命题
”的否命题是真命题
(3)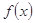 是(
是(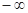 ,0)∪(0,
,0)∪(0,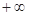 )上的奇函数,
)上的奇函数,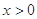 时的解析式是
时的解析式是 ,则
,则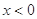 的解析式为
的解析式为
其中正确的说法的个数是().
| A.0个 | B.1个 | C.2个 | D.3个 |
用数学归纳法证明“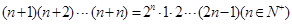 时,从“
时,从“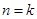 到
到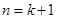 ”时,左边应增添的式子是().
”时,左边应增添的式子是().
A.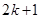 |
B.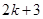 |
C.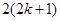 |
D. |
若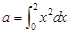 ,
,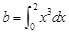 ,
,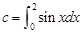 ,则
,则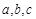 的大小关系是( ).
的大小关系是( ).
A.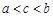 |
B.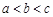 |
C.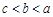 |
D.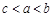 |
以下说法,正确的个数为().
①公安人员由罪犯的脚印的尺寸估计罪犯的身高情况,所运用的是类比推理.
②农谚“瑞雪兆丰年”是通过归纳推理得到的.
③由平面几何中圆的一些性质,推测出球的某些性质这是运用的类比推理.
④个位是5的整数是5的倍数,2375的个位是5,因此2375是5的倍数,这是运用的演绎推理.
| A.0 | B.2 | C.3 | D.4 |
设偶函数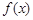 在
在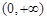 上为减函数,且
上为减函数,且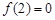 ,则不等式
,则不等式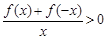 的解集为().
的解集为().
A.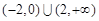 |
B.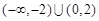 |
C.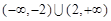 |
D.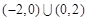 |