已知函数
(1)若 在
在 处取得极值,求
处取得极值,求 的单调递增区间;
的单调递增区间;
(2)若 在区间
在区间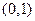 内有极大值和极小值,求实数
内有极大值和极小值,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知集合 ,集合
,集合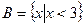 .
.
(1)求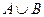 ;
;
(2)求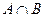 ;
;
(3)求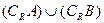
已知函数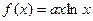 图像上点
图像上点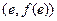 处的切线与直线
处的切线与直线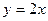
平行(其中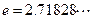 ),
),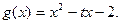 (I)求函数
(I)求函数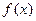 的解析式;
的解析式;
(II)求函数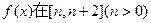 上的最小值;
上的最小值;
(III)对一切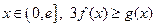 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。
已知椭圆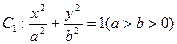 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中
F2也是抛物线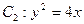 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且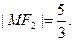
(I)求椭圆C1的方程;(II)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线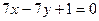 上,求直线AC的方程。
上,求直线AC的方程。
本题满分13分)已知等差数列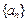 的首项
的首项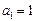 ,公差
,公差 .且
.且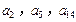 分别是等比数列
分别是等比数列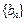 的
的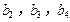 .(1)求数列
.(1)求数列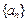 与
与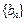 的通项公式;
的通项公式;
(2)设数列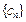 对任意自然数
对任意自然数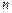 均有:
均有: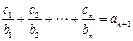 成立.求
成立.求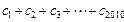 的值。
的值。
如图5,已知直角梯形 所在的平面
所在的平面
垂直于平面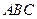 ,
,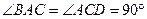 ,
,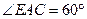 ,
, .(1)在直线
.(1)在直线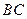 上是否存在一点
上是否存在一点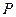 ,使得
,使得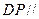 平面
平面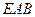 ?请证明你的结论;
?请证明你的结论;
(2)求平面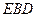 与平面
与平面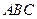 所成的锐二面角
所成的锐二面角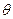 的余弦值。
的余弦值。