（本小题满分12分）
已知函数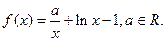
（Ⅰ）若曲线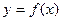
在
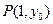处的切线平行于直线
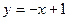，求函数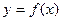的单调区间；
（Ⅱ）若函数
在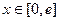
上有两个零点，求实数
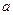的取值范围。
请考生在第（22）、（23）、（24）三题中任选一题作答，如果多做，则按所做的第一题计分，作答时请在答题纸上所选题目题号的方框内打“√”。
已知圆C同时满足下列三个条件:①圆心在直线x-3y=0上;
②与y轴相切;③在x轴上截得的弦长AB为42.求圆C的一般方程.
下列方程能否表示圆?若能表示圆,求出圆心和半径.
(1)2x2+y2-7y+5=0;
(2)x2-xy+y2+6x+7y=0;
(3)x2+y2-2x-4y+10=0;
(4)2x2+2y2-5x=0.
已知一曲线是与两个定点O(0,0)、A(3,0)距离的比为
的点的轨迹,求出曲线的方程.
已知圆的方程x2+y2+2(a-1)x+a2-4a+1=0,若点(-1，-1)在圆外,求实数a的取值范围.
求与x轴相切,圆心在直线3x-y=0上,且被直线x-y=0所截弦长为27的圆的方程.