如图,四边形ABCD是正方形,PB^平面ABCD,MA^平面ABCD,
PB=AB=2MA. 求证:(1)平面AMD∥平面BPC;(2)平面PMD^平面PBD.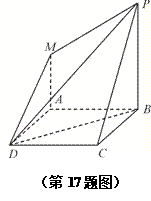
已知函数
(1)求函 数
数 的定义域;
的定义域;
(2)求证:函数 是增函数;
是增函数;
(3)求函数 的最小值.
的最小值.
设定义在 上的奇函数
上的奇函数 是减函数,若
是减函数,若
 ,求实数
,求实数 的取值范围.
的取值范围.
已知集合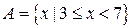 ,
, ,求
,求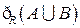 ,
,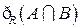 ,
,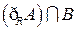 ,
,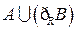 .
.
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;( 6分)
(2)设cn=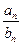 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如下表:
| 资金 |
单位产品所需资金(百元) |
||
| 空调机 |
洗衣机 |
月资金供应量(百元) |
|
| 成本 |
30 |
20 |
300 |
| 劳动力(工资) |
5 |
10 |
110 |
| 单位利润 |
6 |
8 |
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?