如图,一水渠的横断面是抛物线形，O是抛物线的顶点,口宽EF=4米，高3米建立适当的平面直角坐标系，求抛物线方程.现将水渠横断面改造成等腰梯形ABCD，要求高度不变，只挖土，不填土，求梯形ABCD的下底AB多大时，所挖的土最少？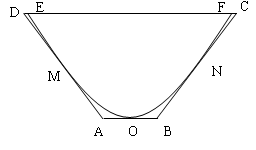 
(本题满分12分)
求焦点为(-5,0)和(5,0)，且一条渐近线为
的双曲线的方程．
已知常数a>0，向量c=（0，a），i=（1，0），经过原点O以c+λi为方向向量的直线与经过定点A（0，a）以i－2λc为方向向量的直线相交于点P，其中λ∈R.试问：是否存在两个定点E、F，使得|PE|+|PF|为定值.若存在，求出E、F的坐标；若不存在，说明理由.
如图，在Rt△ABC中，已知BC=a，若长为2a的线段PQ以点A为中点，问
的夹角
取何值时
的值最大？并求出这个最大值.
四边形ABCD中，
＝ａ，
＝ｂ，
＝с，
＝ｄ，且ａ·ｂ＝ｂ·с＝с·ｄ＝ｄ·ａ，试问四边形ABCD是什么图形?
设两个向量e1，e2，满足|e1|＝2，|e2|＝1，e1与e2的夹角为
.若向量2te1＋7e2与e1＋te2的夹角为钝角，求实数t的范围．