某食品 厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为
厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为 元(
元( 为常数,且
为常数,且 ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为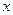 元(
元(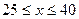 ),根据市场调查,销售量
),根据市场调查,销售量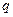 与
与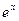 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
(Ⅰ)求该工厂的每日利润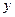 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价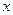 元的函数关系式;
元的函数关系式;
(Ⅱ)若 ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价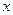 为多少元时,该工厂的利润
为多少元时,该工厂的利润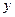 最大,并求最大值.
最大,并求最大值.
(本小题满分12分)在 中,
中,  分别是角
分别是角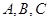 的对边,且
的对边,且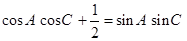 .
.
(1)求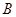 的大小;
的大小;
(2)若 ,
,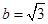 ,求
,求 的面积.
的面积.
(本小题满分12分)设函数
(1)写出函数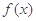 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)当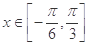 时,函数
时,函数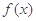 的最大值与最小值的和为
的最大值与最小值的和为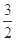 ,求实数
,求实数 的值.
的值.
(本小题满分7分) 选修4—5:不等式选讲
已知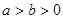 ,且
,且 .
.
(Ⅰ)试利用基本不等式求 的最小值
的最小值 ;
;
(Ⅱ)若实数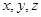 满足
满足 ,求证:
,求证: .
.
(本小题满分7分)选修4—4:极坐标与参数方程
在直角坐标平面内,以坐标原点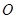 为极点,
为极点,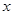 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为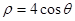 ,直线
,直线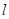 的参数方程为
的参数方程为 (
(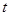 为参数).
为参数).
(Ⅰ)分别求出曲线 和直线
和直线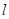 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点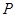 在曲线
在曲线 上,且
上,且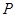 到直线
到直线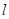 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点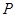 的个数.
的个数.
(本小题满分13分)已知函数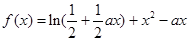 (
( 为常数,
为常数,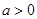 )
)
(1)若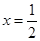 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(2)求证:当 时,
时, 在
在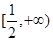 上是增函数;
上是增函数;
(3)若对任意的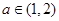 ,总存在
,总存在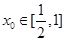 ,使不等式
,使不等式 成立,求正实数
成立,求正实数 的取值范围.
的取值范围.