已知椭圆 ,且C1,C2的公共弦AB过椭圆C1的右焦点。
,且C1,C2的公共弦AB过椭圆C1的右焦点。
(1)求椭圆的焦点坐标及m=0,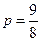 时
时 的焦点坐标;
的焦点坐标;
(2)当AB⊥x轴时,判断抛物线C2的焦点是否在直线AB上;
(3)是否存在m,p的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的m,p的值;若不存在,请说明理由。
古人用天干、地支来表示年、月、日、时的次序.用天干的“甲、丙、戊、庚、壬”和十二支的“子、寅、辰、午、申、戌”相配,用天干的“乙、丁、己、辛、癸”和十二支的“丑、卯、巳、未、酉、亥”相配,共可配成多少组.
某商店失窃,警察审讯4名犯罪嫌疑人.他们当然不会承认是自己偷的,都说是其余3人中的某一个人偷的,他们的供述结果互不相同,共多少种不同的供述结果?
某学校高二年级有12名语文教师、13名数学教师、15名英语教师,市教育局拟召开一个新课程研讨会.
(1)若选派1名教师参会,有多少种派法?
(2)若三个学科各派1名教师参会,有多少种派法?
(3)若选派2名不同学科的教师参会,有多少种派法?
学校举行运动会,有四位同学参加三项不同的比赛
(1)每位同学必须参加一项比赛,有多少种不同的结果?
(2)每项比赛只许一位学生参加,有多少种不同的结果?
锐角三角形ABC中,角A、B、C所对的边分别为a、b、c, ="(a-b,c),"
="(a-b,c),"  =(a-c,a+b),且
=(a-c,a+b),且 与
与 共线。
共线。
(I)求角B的大小;
(II)设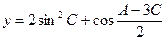 ,求y的最大值及此时∠C的大小。
,求y的最大值及此时∠C的大小。