（本小题满分12分）
如图，平面ABCD⊥平面PAD，△APD是直角三角形，
∠APD=90°，四边形ABCD是直角梯形，其中BC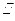
AD，
∠BAD=90°，AD="2" BC，且AB=BC=PD=2，O是AD的中点，E，F分别是PC，OD的中点.
（Ⅰ）求证：EF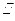平面PBO；
（Ⅱ）求二面角A- PF - E的正切值.
已知f(x)＝x＋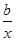
－3，x∈[1，2]．
(1)当b＝2时，求f(x)的值域；
(2)若b为正实数，f(x)的最大值为M，最小值为m，且满足M－m≥4，求b的取值范围．
已知A＝{x|ax－1>0}，B＝{x|x2－3x＋2>0}．
(1)若A∩B＝A，求实数a的取值范围；
(2)若A∩∁RB≠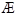
，求实数a的取值范围．
设关于x的不等式x(x－a－1)＜0(a∈R)的解集为M，不等式x2－2x－3≤0的解集为N.
(1)当a＝1时，求集合M；
(2)若M∪N＝N，求实数a的取值范围．
若全集U＝{1，2，3，4，5，6}，M∩N＝N，N＝{1，4}，试求满足条件的集合M的个数．
已知A＝{a＋2，(a＋1)2，a2＋3a＋3}且1∈A，求实数a的值．