(本小题14分)
已知函数 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: ,
, ,其中
,其中 表示函数
表示函数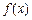 在D上的最小值,
在D上的最小值, 表示函数
表示函数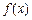 在D上的最大值,若存在最小正整数k,使得
在D上的最大值,若存在最小正整数k,使得 对任意的
对任意的 成立,则称函数
成立,则称函数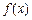 为
为 上的“k阶收缩函数”
上的“k阶收缩函数”
(1)若 ,试写出
,试写出 ,
, 的表达式;
的表达式;
(2)已知函数 试判断
试判断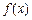 是否为[-1,4]上的“k阶收缩函数”,
是否为[-1,4]上的“k阶收缩函数”,
如果是,求出对应的k,如果不是,请说明理由;
已知 ,函数
,函数 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围
(本小题满分13分)已知椭圆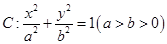 的离心率为
的离心率为 ,右焦点
,右焦点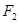 到直线
到直线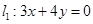 的距离为
的距离为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆右焦点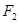 斜率为
斜率为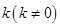 的直线
的直线 与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线
与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线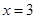 于点M,N,线段MN的中点为P,记直线
于点M,N,线段MN的中点为P,记直线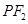 的斜率为
的斜率为 ,求证:
,求证: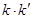 为定值.
为定值.
(本小题满分12分)某市近郊有一块大约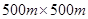 的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.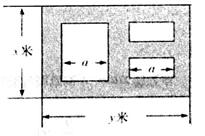
(Ⅰ)分别用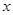 表示
表示 和S的函数关系式,并给出定义域;
和S的函数关系式,并给出定义域;
(Ⅱ)怎样设计能使S取得最大值,并求出最大值.
(本小题满分12分)设等差数列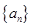 的前
的前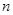 项和为
项和为 .数列
.数列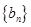 的前
的前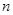 项和为
项和为 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设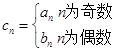 ,求数列
,求数列 的前
的前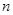 项和
项和 .
.
(本小题满分12分)在如图所示的几何体中,四边形ABCD是等腰梯形,AB//CD,∠ABC=60°,AB=2CB=2.在梯形ACEF中,EF//AC,且 平面ABCD.
平面ABCD.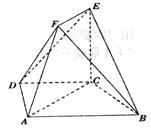
(Ⅰ)求证: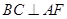 ;
;
(Ⅱ)若二面角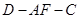 为45°,求CE的长.
为45°,求CE的长.
(本小题满分12分)已知△ABC中的三个内角A,B,C所对的边分别为 ,且满足
,且满足
(Ⅰ)求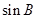 ;(Ⅱ)求△ABC的面积.
;(Ⅱ)求△ABC的面积.