(本小题满分12分)某市近郊有一块大约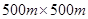 的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.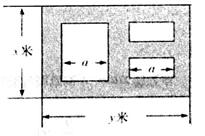
(Ⅰ)分别用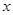 表示
表示 和S的函数关系式,并给出定义域;
和S的函数关系式,并给出定义域;
(Ⅱ)怎样设计能使S取得最大值,并求出最大值.
已知等比数列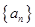 中,
中,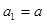 ,
,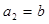 ,
,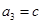 ,
,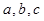 分别为△ABC的三个内角A,B,C的对边,且
分别为△ABC的三个内角A,B,C的对边,且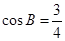 .
.
(1)求数列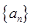 的公比
的公比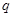 ;
;
(2)设集合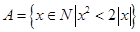 ,且
,且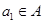 ,求数列
,求数列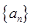 的通项公式.
的通项公式.
某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样,回答问题统计结果如图表所示.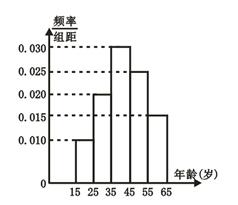
| 组别 |
分组 |
回答正确的人数 |
回答正确的人数占本组的概率 |
| 第1组 |
[15,25) |
5 |
0.5 |
| 第2组 |
[25,35) |
 |
0.9 |
| 第3组 |
[35,45) |
27 |
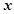 |
| 第4组 |
[45,55) |
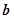 |
0.36 |
| 第5组 |
[55,65) |
3 |
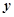 |
(1)分别求出 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价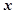 (元) (元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
销量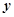 (件) (件) |
90 |
84 |
83 |
80 |
75 |
68 |
(1)根据上表可得回归直线方程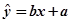 中的
中的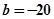 ,据此模型预报单价为10元时的销量为多少件?
,据此模型预报单价为10元时的销量为多少件?
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入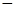 成本)
成本)
随机抽取某中学甲班10名同学,他们的身高(单位:cm)数据是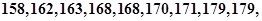
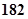 ;乙班10名同学,他们的身高(单位:cm)数据是
;乙班10名同学,他们的身高(单位:cm)数据是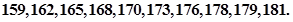
(1)画出甲、乙两班的茎叶图,并说明茎叶图有什么优点和缺点?
(2)根据茎叶图判断哪个班的平均身高较高(不必计算).
函数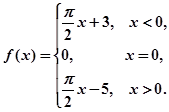 请设计算法框图,要求输入自变量,输出函数值.
请设计算法框图,要求输入自变量,输出函数值.