(本题14分)
(1)将一颗骰子(正方体形状)先后抛掷2次,得到的点数分别记为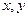 ,
,
求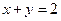 及
及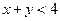 的概率;
的概率;
(2)从区间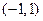 中随机取两个数
中随机取两个数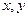 ,求
,求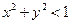 的概率.
的概率.
某渔场养鱼,鱼的重量增长率第一年为400%,以后每年重量增长率都是前一年的三分之一。同时鱼每年要损失预计重量的10%。预计养鱼的费用第一年是鱼苗成本的20%,以后每年的费用M(t)与年数t满足关系式 (其中
(其中 为鱼苗成本,
为鱼苗成本, )。问该渔场的鱼养几年后全部捕捞,鱼的产值高且费用较少(设鱼苗价30元/斤,成鱼市场价7元/斤)。
)。问该渔场的鱼养几年后全部捕捞,鱼的产值高且费用较少(设鱼苗价30元/斤,成鱼市场价7元/斤)。
铁道机车运行1小时所需的成本由两部分组成,固定部分为 元,变动部分与运行速度V(千米/小时)的平方成正比。比例系数为k(k≠0)。如果机车匀速从甲站开往乙站,为使成本最省应以怎样的速度运行?
元,变动部分与运行速度V(千米/小时)的平方成正比。比例系数为k(k≠0)。如果机车匀速从甲站开往乙站,为使成本最省应以怎样的速度运行?
某市1994年底人口为20万,人均住房面积为8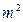 ,计划1998年底人均住房面积达10
,计划1998年底人均住房面积达10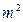 。如果该市每年人口平均增长率控制在1%,要实现上述计划,这个城市每年平均至少要新增住房面积多少万
。如果该市每年人口平均增长率控制在1%,要实现上述计划,这个城市每年平均至少要新增住房面积多少万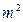 (结果以万
(结果以万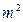 为单位,保留两位小数)。
为单位,保留两位小数)。
某企业在今年年初向银行贷款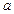 万元,年利率为
万元,年利率为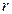 ;从今年年末开始,每年末向银行偿还一定的金额,预计五年内还清,问每年末平均偿还的金额应是多少?
;从今年年末开始,每年末向银行偿还一定的金额,预计五年内还清,问每年末平均偿还的金额应是多少?
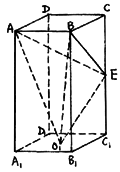
已知:如图,长方体ABCD—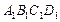 中,AB=BC=4,
中,AB=BC=4,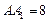 ,E为
,E为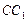 的中点,
的中点,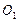 为下底面正方形的中心.求:(I)二面角C—AB—
为下底面正方形的中心.求:(I)二面角C—AB—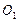 的正切值;
的正切值;
(II)异面直线AB与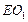 所成角的正切值;
所成角的正切值;
(III)三棱锥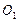 ——ABE的体积.
——ABE的体积.
 |