((本题15分)
已知直线l的方程为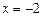 ,且直线l与x轴交点
,且直线l与x轴交点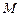 ,圆
,圆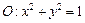 与x轴交
与x轴交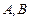 两点.
两点.
(1)过M点的直线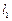 交圆于
交圆于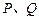 两点,且圆孤
两点,且圆孤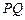 恰为圆周的
恰为圆周的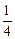 ,求直线
,求直线 的方程;
的方程;
(2)求以l为准线,中心在原点,且与圆O恰有两个公共点的椭圆方程;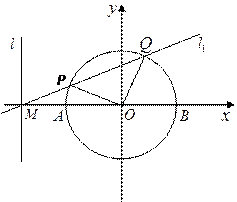 (3)过M点作直线
(3)过M点作直线 与圆相切于点
与圆相切于点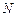 ,设(2)中椭圆的两个焦点分别为
,设(2)中椭圆的两个焦点分别为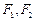 ,求三角形
,求三角形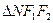 面积.
面积.
已知函数f(x)=ln x+ax(a∈R).
(1)求f(x)的单调区间;
(2)设g(x)=x2-4x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
已知函数f(x)= +ln x.
+ln x.
(1)当a= 时,求f(x)在[1,e]上的最大值和最小值;
时,求f(x)在[1,e]上的最大值和最小值;
(2)若函数g(x)=f(x)- x在[1,e]上为增函数,求正实数a的取值范围.
x在[1,e]上为增函数,求正实数a的取值范围.
设f(x)=aln x+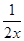 +
+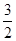 x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
(1)求a的值;
(2)求函数f(x)的极值.
已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?