如图，在梯形ABCD中，AB‖CD，∠A=
，AB=3，CD=6，BE⊥BC交直线AD于点E. 
（1）当点E与D恰好重合时，求AD的长；
（2）当点E在边AD上时（E不与A、D重合），设AD=x，ED=y，试求y关于x的函数关系式，并写出定义域；
（3）问：是否可能使△ABE、△CDE与△BCE都相似？若能，请求出此时AD的长；若不能，请说明理由.
按语句画图。
（1）作锐角∠AOB；
（2）作射线OC⊥OA，OD⊥OB；
（3）判断∠AOB与∠COD的关系，并且说明理由
解方程：
（1）
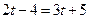
（2）
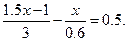
(3)关于
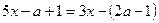的方程
与方程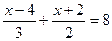
同解,求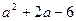
计算：
（1）
（2）
如图，已知∆ABC中，
，
，D是AB上一动点，DE∥BC，交AC于E，将四边形BDEC沿DE向上翻折，得四边形
，
与AB、AC分别交于点M、N.
（1）证明：∆ADE 
；
（2）设AD为x，梯形MDEN的面积为y，试求y与x的函数关系式. 当x为何值时y有最大值？
如图，以线段
为直径的⊙
交线段
于点
，点
是弧AE的中点，
交于点
，
°，
，
．
（1）求
的度数；
（2）求证：BC是⊙的切线；
（3）求MD的长度．