（本小题满分14分）有人玩掷正四面体骰子走跳棋的游戏，已知正四面体骰子四个面上分别印有
，棋盘上标有第0站、第1站、第2站、…、第100站．一枚棋子开始在第0站，棋手每掷一次骰子，若掷出后骰子为
面，棋子向前跳2站，若掷出后骰子为
中的一面，则棋子向前跳1站，直到棋子跳到第99站（胜利大本营）或第100站（失败大本营）时，该游戏结束．设棋子跳到第n站的概率为
（
）．
（Ⅰ）求
；
（Ⅱ）求证：
；
（Ⅲ）求玩该游戏获胜的概率．
如图，在
中，
是
上的高，沿
把折起，使
.
（Ⅰ）证明：平面ＡＤＢ⊥平面ＢＤＣ；
（Ⅱ）设Ｅ为ＢＣ的中点，求AE与DB所成角的余弦值.
. 已知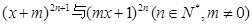
的展开式中含xn项的系数相等，求实数m的取值范围.
（本小题满分12分．其中（Ⅰ）小问6分，（Ⅱ）小问6分）
已知
，数列{an}满足：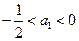
,
．
（Ⅰ）求证：
；
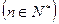（Ⅱ）判断an与an+1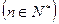的大小，并说明理由．
（本小题满分12分．其中（Ⅰ）小问5分，（Ⅱ）小问7分）
已知函数
，
．
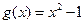（Ⅰ）求函数
的最大值；
（Ⅱ）对于一切正数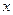
，恒有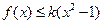
成立，求实数
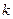的取值组成的集合．
（本小题满分12分．其中（Ⅰ）小问6分，（Ⅱ）小问6分）
如图，已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，PD⊥底面ABCD，E、F分别为棱BC、AD的中点．
（Ⅰ）若PD=1，求异面直线PB和DE所成角的余弦值；
（Ⅱ）若二面角P-BF-C的余弦值为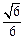
，求四棱锥P-ABCD的体积