如图所示,宽度为L=0.20 m的足够长的平行光滑金属导轨固定在绝缘水平面上,导轨的一端连接阻值为R=1.0Ω的电阻。导轨所在空间存在竖直向下的匀强磁场,磁感应强度大小为B="0.50" T。一根质量为m=10g的导体棒MN放在导轨上与导轨接触良好,导轨和导体棒的电阻均可忽略不计。现用一平行于导轨的拉力拉动导体棒沿导轨向右匀速运动,运动速度v="10" m/s,在运动过程中保持导体棒与导轨垂直。求:
(1)在闭合回路中产生的感应电流的大小;
(2)作用在导体棒上的拉力的大小;
(3)当导体棒移动30cm时撤去拉力,求整个过程中电阻R上产生的热量。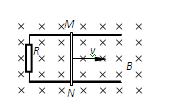
一列火车做匀变速直线运动驶来,一人在火车旁观察火车的运动,发现相邻的两个10s内,列车从他跟前驶过8节车厢和6节车厢,每节车厢长8m,求:
(1)火车的加速度;
(2)人开始观察时火车的速度大小.
用滴水法可以测定重力加速度的值。方法是:在自来水龙头下面固定一块挡板A,使水一滴一滴断续地滴落到挡板上,仔细调节水龙头,使得耳朵刚好听到前一水滴滴在挡板上的声音的同时,下一水滴刚好开始下落.首先量出水龙头口离挡板的高度h,再用秒表计时,计时方法是:当听到某一水滴滴在挡板上的声音的同时,开启秒表开始计时,并数“1”,以后每听到一声水滴声,依次数“2、3、4……”,一直数到“n”时,按下秒表按钮停止计时,读出秒表的示数为t。写出用上述测量计算重力加速度g的表达式为g =。
甲车以加速度3m/s2由静止开始作匀加速直线运动,乙车落后2s钟在同一地点由静止开始,以加速度4m/s2作匀加速直线运动,两车的运动方向相同,求:
(1)在乙车追上甲车之前,两车距离的最大值是多少?
(2)乙车出发后经多长时间可追上甲车?
一列火车做匀变速直线运动驶来,一人在火车旁观察火车的运动,发现相邻的两个10s内,列车从他跟前驶过8节车厢和6节车厢,每节车厢长8m,求:
(1)火车的加速度;
(2)人开始观察时火车的速度大小.
用滴水法可以测定重力加速度的值。方法是:在自来水龙头下面固定一块挡板A,使水一滴一滴断续地滴落到挡板上,仔细调节水龙头,使得耳朵刚好听到前一水滴滴在挡板上的声音的同时,下一水滴刚好开始下落.首先量出水龙头口离挡板的高度h,再用秒表计时,计时方法是:当听到某一水滴滴在挡板上的声音的同时,开启秒表开始计时,并数“1”,以后每听到一声水滴声,依次数“2、3、4……”,一直数到“n”时,按下秒表按钮停止计时,读出秒表的示数为t。写出用上述测量计算重力加速度g的表达式为g = 。