在如图17所示的坐标系中,x 轴沿水平方向,y 轴沿竖直方向.第二象限内存在沿 y 轴负方向的匀强电场,在第三象限内存在垂直 xy 平面(纸面)向里的匀强磁场.一质量为m 、电量为q的带正电粒子(不计重力),从y 轴上的A点以v0的初速度沿x 轴负方向进入第二象限,之后到达x轴上x= – 2h处的B点,带电粒子在 B点的速度方向与x轴负方向成 450 角,进入第三象限后粒子做匀速圆周运动,恰好经过y 轴上y = –2h处的C点。求:
⑴ 粒子到达B点时速度大小;
⑵ 第二象限中匀强电场的电场强度的大小;
⑶ 第三象限中磁感应强度的大小和粒子在磁场中的运动时间.
如图15所示,PQ、MN两极板间存在匀强电场,两极板间电势差为U、间距为d,MN极板右侧虚线区域内有垂直纸面向内的匀强磁场。现有一初速度为零、带电量为q、质量为m的离子从PQ极板出发,经电场加速后,从MN上的小孔A垂直进入磁场区域,并从C点垂直于虚线边界射出。求:
(1)离子从小孔A射出时速度v0;
(2)离子带正电还是负电?C点离MN板的距离?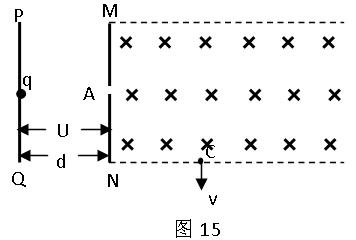
一定质量的理想气体从状态A变化到状态B,再变化到状态C,其状态变化过程的p-V图象如图所示。已知该气体在状态A时的温度为27℃。则:
(1)该气体在状态B、C时的温度分别为多少℃?
(2)该气体从状态A到状态C的过程中内能的变化量是多大?
一辆汽车正以15m/s的速度行驶,因发生紧急情况关闭油门刹车,刹车后做匀减速直线运动,加速度大小为3m/s2,问
(1)刹车3秒后汽车的速度大小
(2)刹车6秒内的位移
一颗手榴弹在5m高处以v0=10m/s的速度水平飞行时,炸裂成质量比为3:2的两小块,质量大的以100m/s的速度反向飞行,求两块落地点的距离。(g取10m/s2)
质量为10g的小球甲在光滑的水平桌面上以30cm/s的速率向右运动,恰遇上质量为50g的小球乙以10cm/s的速率向左运动,碰撞后,小球乙恰好静止。那么,碰撞后小球甲的速度多大?方向如何?